当x 取值x1，x2，…，xn 时，得y 的一组观测值y1，y2，…，yn，

称为y1，y2，…，yn，的总偏差平方和（total sum of squares），它的大小反映了观测值y1，y2，…，yn的分散程度.对Q总进行分析

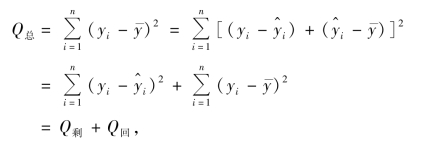
其中

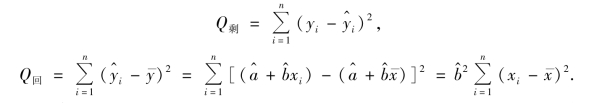
Q剩称为剩余平方和（residual sum of squares），它反映了观测值yi 偏离回归直线的程度，这种偏离是由试验误差及其他未加控制的因素引起的.可证明是σ2 的无偏估计.

Q回为回归平方和（regression sum of squares），它反映了回归值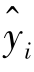（i=1，2，…，n）的分散程度，它的分散性是因x 的变化而引起的，并通过x 对y 的线性影响反映出来.因此的分散性来源于x1，x2，…，xn 的分散性.

通过对Q剩、Q回的分析，y1，y2，…，yn 的分散程度Q总的两种影响可以从数量上区分开来.Q剩较小时，偏离回归直线的程度小.Q回较大时，分散程度大.因而Q回与Q剩的比值反映了这种线性相关关系与随机因素对y 的影响的大小.比值越大，线性相关性越强.

可证明统计量

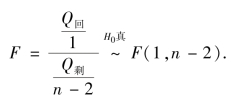(www.daowen.com)

给定显著性水平α，若F≥Fα，则拒绝假设H0，即认为在显著性水平α 下，y 对x 的线性相关关系是显著的.反之，则认为y 对x 没有线性相关关系，即所求线性回归方程无实际意义.检验时，可使用方差分析表10.4.

表10.4

其中

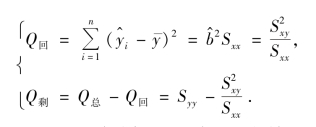
例10.3　在显著性水平α=0.05，检验例10.1 中的回归效果是否显著？

解　由例10.1 知

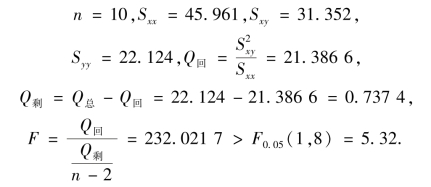
故拒绝H0，即两变量的线性相关关系是显著的.