最小二乘法是估计未知参数的一种重要方法，现用它来求一元线性回归模型中a 和b 的估计.

最小二乘法的基本思想是：对一组观察值（x1，y1），（x2，y2），…，（xn，yn），使误差εi=yi-（a+bxi）的平方和

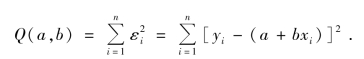
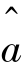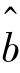达到最小的和作为a 和b 的估计，称其为最小二乘估计（least squares estimate）.直观地说，平面上直线很多，选取哪一条最佳呢？很自然的一个想法是，当点（xi，yi），i=1，2，…，n，与某条直线的偏差平方和比它们与任何其他直线的偏差平方和都要小时，这条直线便能最佳地反映这些点的分布状况，并且可以证明，在某些假设下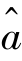， 和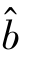是所有线性无偏估计中最好的.

根据微分学的极值原理，可将Q（a，b）分别对a，b 求偏导数，并令它们等于零，得到方程组

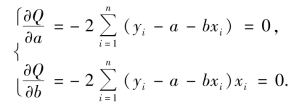
即

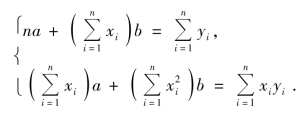
上式称为正规方程组.

由于xi 不全相同，正规方程组的参数行列式

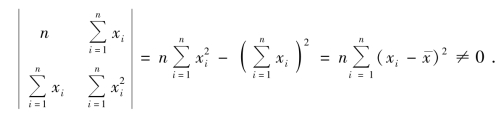
故正规方程组有唯一解

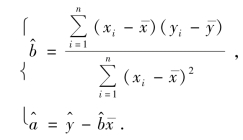
于是，所求的线性回归方程为

若将代入上式，则线性回归方程亦可写为

上式表明，对于样本观察值（x1，y1），（x2，y2），…，（xn，yn），回归直线通过散点图的几何中心.回归直线是一条过点，斜率为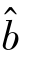的直线.(www.daowen.com)

上述确定回归直线所依据的原则是使所有观测数据的偏差平方和达到最小值.按照这个原理确定回归直线的方法称为最小二乘法.“二乘”是指Q 是二乘方（平方）的和.如果y 是正态变量，也可用极大似然估计法得出相同的结果.

为了计算上的方便，引入下述记号

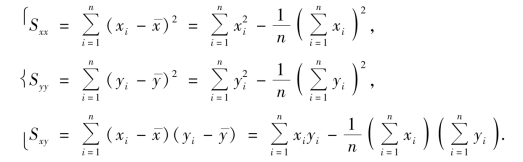
这样，a，b 的估计可写成

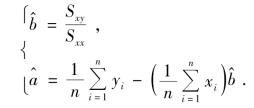
例10.1　某企业生产一种毛毯，1—10 月份的产量x 与生产费用支出y 的统计资料见表10.1.求y 关于x 的线性回归方程.

表10.1

解　为求线性回归方程，将有关计算结果列表，见表10.2.

表10.2

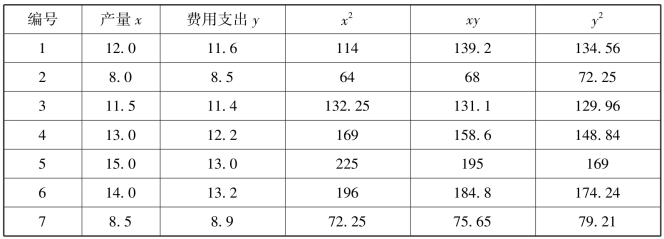
续表

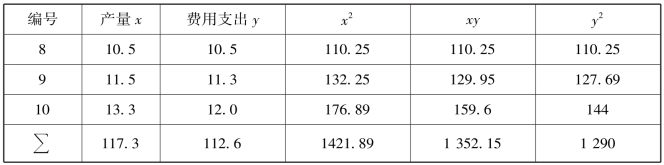
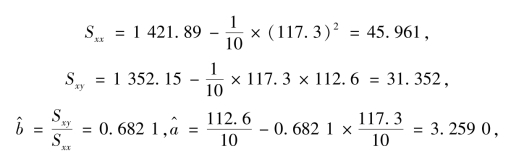
故回归方程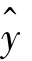：=3.259 0+0.682 1x.

需要指出的是，当我们求得了y 的最小估计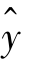后，就可建立回归方程，从而可以利用它对指标进行预报和控制.然而，最小二乘法得出的结果有时可能不适用.因此，为了了解预测的精度及控制生产的需要进行检验，通常是求σ2 估计.