正交试验设计的极差分析简便易行，计算量小，也较直观，但极差分析精度较差，判断因素的作用时缺乏一个定量的标准.这些问题要用方差分析解决.

设有一试验，使用正交表Lp（nm），试验的p 个结果为y1，y2，…，yp，记

为试验的p 个结果的总变差.

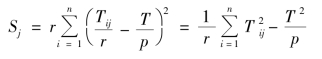
为第j 列上安排因素的变差平方和，其中r=.可证明

即总变差为各列变差平方和之和，且ST 的自由度为p-1，Sj 的自由度为n-1.当正交表的所有列没被排满因素时，即有空列时，所有空列的Sj 之和就是误差的变差平方和Sj，这时Se 的自由度fe 也为这些空列自由度之和.当正交表的所有列都排有因素时，即无空列时，取Sj 中的最小值作为误差的变差平方和Se.

从以上分析知，在使用正交表Lp（nm）的正交试验方差分析中，对正交表所安排的因素选用的统计量为

当因素作用不显著时，

其中第j 列安排的是被检因素.(www.daowen.com)

在实际应用时，先求出各列的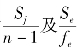，若某个还小时，则这第j 列就可当作误差列并入Se 中去，这样使误差Se 的自由度增大，在作F 检验时会更灵敏，将所有可当作误差列的Sj 全并入Se 后得新的误差变差平方和，记为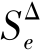，其相应的自由度为，这时选用统计量

例9.9　对例9.8 的表9.23 作方差分析.

解　由表9.23 的最后一行的极差值Rj，利用公式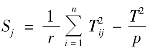，得表9.24.

表9.24

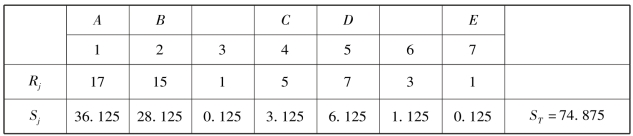
表9.24 中第3，6 列为空列，因此Se=S3+S6=1.250，其中fe=1+1=2，所以Se/fe=0.625，而第7 列的S7=0.125，S7/f7=0.125/1=0.125 比Se/fe 小，故将它并入误差.

=Se+S7=1.375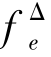，=3.整理成方差分析表9.25.

表9.25

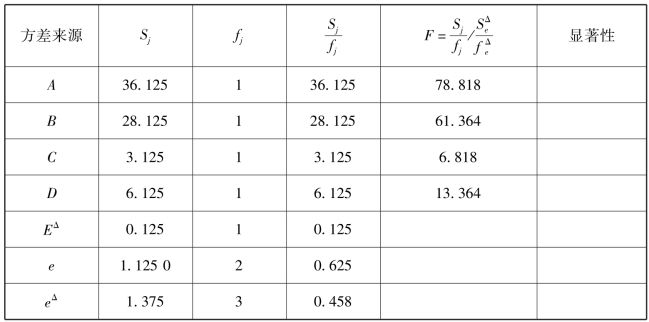
由于F0.05（1，3）=10.13，F0.01（1，3）=34.12，故因素A，B 作用高度显著，因素C 作用不显著，因素D 作用显著，这与前面极差分析的结果是一致的.F 检验法要求选取Se，且希望fe 要大，故在安排试验时，适当留出些空列是有好处的.在前面的方差分析中，讨论因素A 和B 的交互作用A×B.这类交互作用在正交试验设计中同样有表现，即一个因素A 的水平对试验结果指标的影响同另一个因素B 的水平选取有关.当试验考虑交互作用时，也可用前面讲的基本方法来处理.本章就不再介绍了.