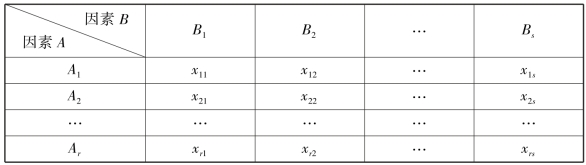
在双因素试验中，如果对每一对水平的组合（Ai，Bj）只做一次试验，即不重复试验，所得结果见表9.13.

表9.13

这时=xijk，SE=0，SE 的自由度为0，故不能利用双因素等重复试验中的公式进行方差分析.但是，如果我们认为A，B 两因素无交互作用，或已知交互作用对试验指标影响很小，则可将SA×B取作SE，仍可利用等重复的双因素试验对因素A，B 进行方差分析.对这种情况下的数学模型及统计分析表示如下：

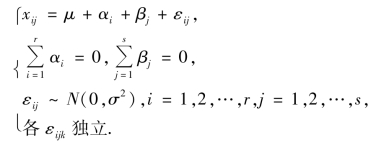
要检验的假设有以下两个

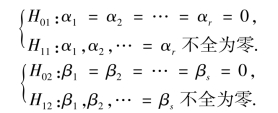
记

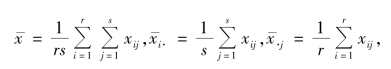
平方和分解公式为

其中

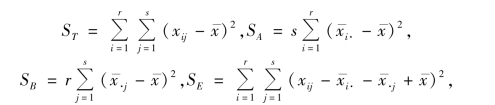
分别为总平方和、因素A，B 的效应平方和和误差平方和.

取显著性水平为α，当H01成立时，

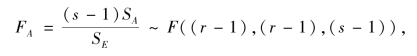
H01拒绝域为(www.daowen.com)

当H02成立时，

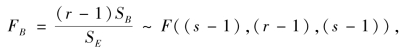
H02拒绝域为

得方差分析表9.14.

表9.14

例9.6　测试某种钢不同含铜量在各种温度下的冲击值（单位：kg·m·cm -1），表9.15列出了试验的数据（冲击值），问试验温度、含铜量对钢的冲击值的影响是否显著（α=0.01）？

表9.15

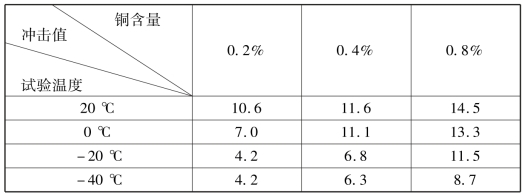
解　由已知，r=4，s=3，需检验假设H01，H02，经计算得方差分析表9.16.

表9.16

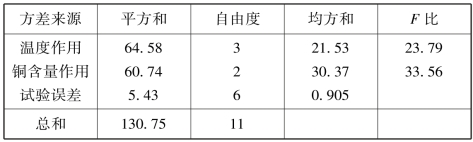
由于F0.01（3，6）=9.78 <FA，拒绝H01.F0.01（2，6）=10.92 <FB，拒绝H02.

检验结果表明，试验温度、含铜量对钢冲击值的影响是显著的.