设有两个因素A，B 作用于试验的指标，因素A 有r 个水平A1，A2，…，Ar，因素B 有s 个水平B1，B2，…，Bs，现对因素A，B 的水平的每对组合（Ai，Bj）（i=1，2，…，r；j=1，2，…s）都作t（t≥2）次试验（称为等重复试验），得到表9.8 的结果

表9.8

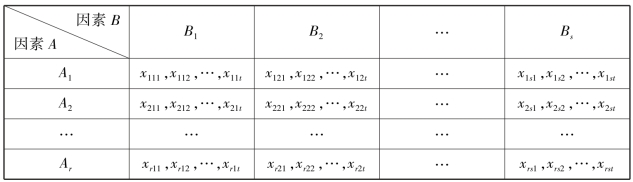
设xijk ~N（μij，σ2）（i=1，2，…，r；j=1，2，…，s；k=1，2，…，t），各xijk独立.这里μij，σ2 均为未知参数，或写为

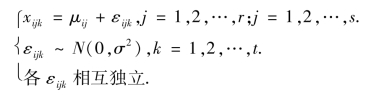
记

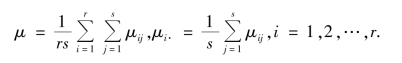
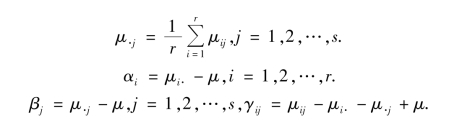
于是

称μ 为总平均，αi 为水平Ai 的效应，βj 为水平Bj 的效应，γij为水平Ai 和水平Bj 的交互效应，这是由Ai，Bj 搭配起来联合作用而引起的.

易知

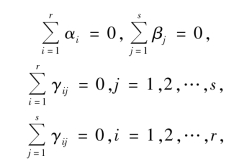
这样双因素方差分析的数学模型可写成

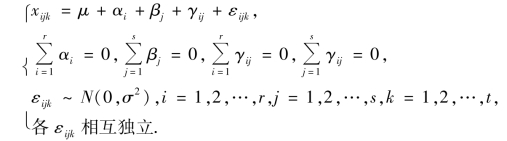
其中μ，αi，βj，γij及σ2 都为未知参数.

上式就是我们所要研究的双因素试验方差分析的数学模型.我们要检验因素A，B 及交互作用A×B 是否显著.要检验以下3 个假设

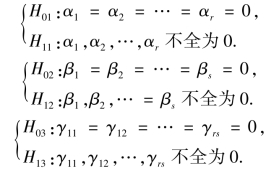
类似于单因素情况，对这些问题的检验方法也是建立在平方和分解上的.记

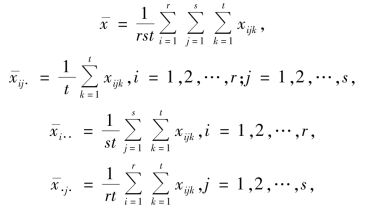
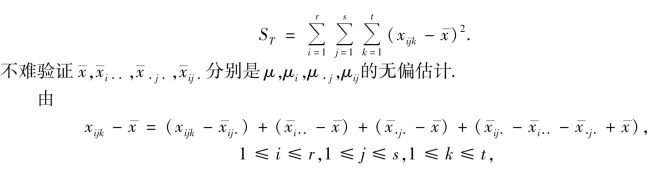
得平方和的分解式

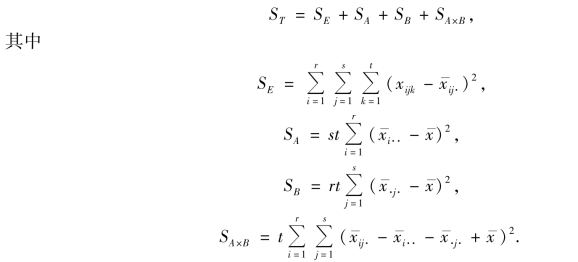
SE 称为误差平方和，SA，SB 分别称为因素A，B 的效应平方和，SA×B称为A，B 交互效应平方和.

当H01：α1=α2=…=αr=0 为真时，

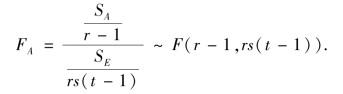(www.daowen.com)

当假设H02为真时，

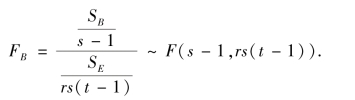
当假设H03为真时，

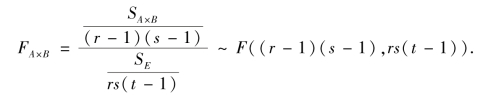
当给定显著性水平α 后，假设H01，H02，H03的拒绝域分别为

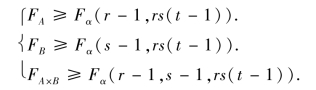
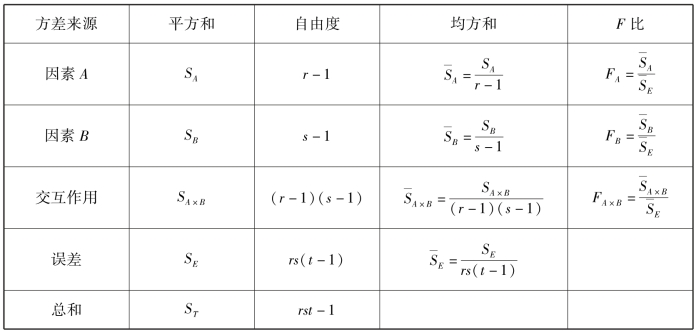
经过上面的分析和计算，可得出双因素试验的方差分析表9.9.

表9.9

在实际中，与单因素方差分析类似可按以下较简便的公式来计算ST，SA，SB，SA×B，SE.

记

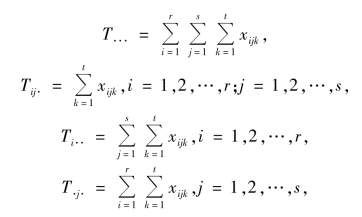
即有

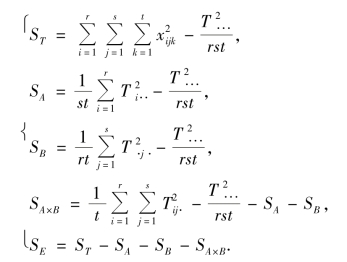
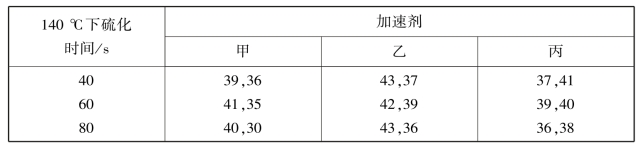
例9.5　用不同的生产方法（不同的硫化时间和不同的加速剂）制造的硬橡胶的抗牵拉强度（单位：kg·cm -2）的观察数据如表9.10 所示.试在显著水平0.10 下分析不同的硫化时间（A），加速剂（B）以及它们的交互作用（A×B）对抗牵拉强度有无显著影响.

表9.10

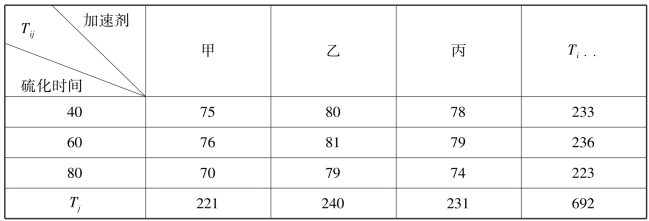
解　按题意，需检验假设H01，H02，H03.r=s=3，t=2，T，Tij，Ti，Tj 的计算见表9.11.

表9.11

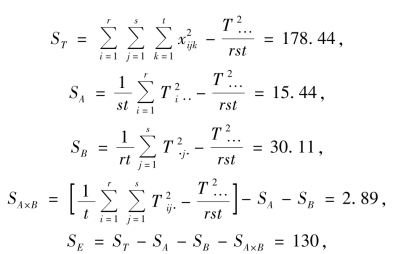
得方差分析表9.12.

表9.12

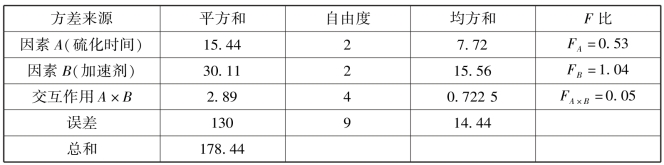
由于F0.10（2，9）=3.01 >FA，F0.10（2，9） >FB，F0.10（4，9）=2.69 >FA×B，因而接受假设H01，H02，H03，即硫化时间、加速剂以及它们的交互作用对硬橡胶的抗牵拉强度的影响不显著.