当H0 成立时，设xij ~N（μj，σ2）（i=1，2，…，nj，j=1，2，…，s）且相互独立，利用抽样分布的有关定理，我们有

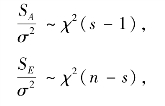
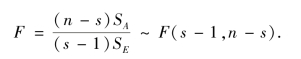
于是，对于给定的显著性水平α（0 <α<1），由于

由此得检验问题的拒绝域为

由样本值计算F 的值，若F≥Fα，则拒绝H0，即认为水平的改变对指标有显著性的影响.若F<Fα，则接受原假设H0，即认为水平的改变对指标无显著影响.

上面的分析结果可排成表9.4 的形式，称为方差分析表.

表9.4

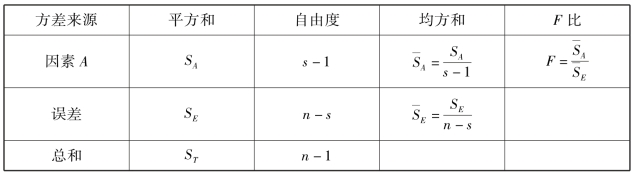
当F≥F0.05（s-1，n-s）时，称为显著.当F≥F0.01（s-1，n-s）时，称为高度显著（极显著）.

在实际中，我们可以按以下较简便的公式来计算ST，SA 和SE，记

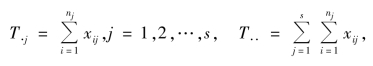
即有

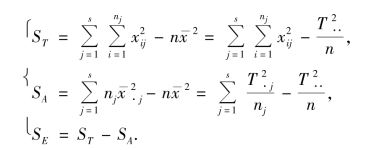
例9.3　如上所述，在例9.1 中需检验假设

(www.daowen.com)

给定α=0.05，完成这一假设检验.

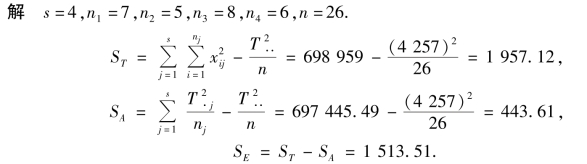
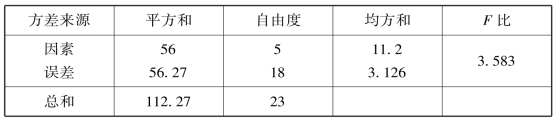
得方差分析表9.5.

表9.5

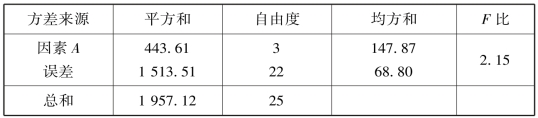
因

则接受H0，即认为4 种生铁试样的热疲劳性无显著差异.

例9.4　如上所述，在例9.2 中需检验假设

试取α=0.05，α=0.01，完成这一假设检验.

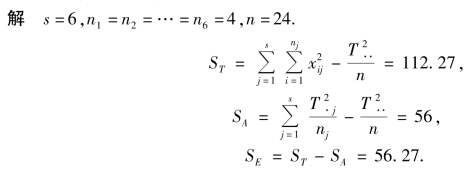
得方差分析表9.6.故浸泡水的温度对缩水率有显著影响，但不能说有高度显著的影响.

表9.6

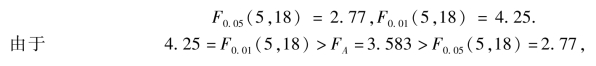
本节的方差分析是在这两项假设下，检验各个正态总体均值是否相等.一是正态性假设，假定数据服从正态分布.二是等方差性假设，假定各正态总体方差相等.由大数定律及中心极限定理，以及多年来的方差分析应用，知正态性和等方差性这两项假设是合理的.