例9.1 某试验室对钢锭模进行选材试验.其方法是将试件加热到700 ℃后,投入20 ℃的水中急冷,这样反复进行到试件断裂为止,试验次数越多,试件质量越好.试验结果见表9.1.
表9.1
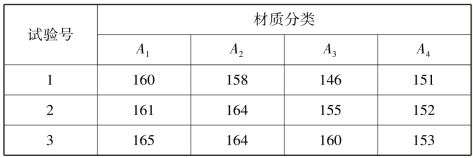
续表
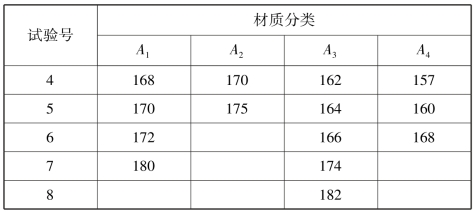
试验的目的是确定4 种生铁试件的抗热疲劳性能是否有显著差异.这里,试验的指标是钢锭模的热疲劳值,钢锭模的材质是因素,4 种不同的材质表示钢锭模的4 个水平,这项试验称为4 水平单因素试验.
例9.2 考察一种人造纤维在不同温度的水中浸泡后的缩水率,在40 ℃,50 ℃,…,90 ℃的水中分别进行4 次试验.得到该种纤维在每次试验中的缩水率如表9.2.试问浸泡水的温度对缩水率有无显著的影响?
表9.2
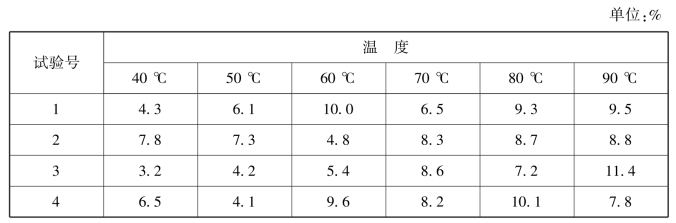
这里试验指标是人造纤维的缩水率,温度是因素,这项试验为6 水平单因素试验.
单因素试验的一般数学模型为:因素A 有s 个水平A1,A2,…,As,在水平Aj(j=1,2,…,s)下进行nj(nj≥2)次独立试验,得到表9.3 的结果:
表9.3

假定各水平Aj(j=1,2,…,s)下的样本xij ~N(μj,σ2),i=1,2,…,nj,j=1,2,…,s 且相互独立,故xij-μj 可看成随机误差,它们是试验中无法控制的各种因素所引起的.记xij-μj=εij,则(https://www.daowen.com)
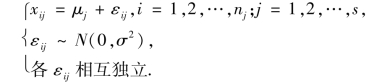
其中μj 与σ2 均为未知参数.上式称为单因素试验方差分析的数学模型.方差分析的任务是对于上述数学模型,检验s 个总体N(μ1,σ2),…,N(μs,σ2)的均值是否相等,即检验假设

为将上述问题写成便于讨论的形式,采用记号
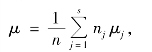
其中n=![]() ,μ 表示μ1,μ2,…,μs 的加权平均,μ 称为总平均.
,μ 表示μ1,μ2,…,μs 的加权平均,μ 称为总平均.
![]()
δj 表示水平Aj 下的总体平均值与总平均的差异.习惯上将δj 称为水平Aj 的效应.利用这些记号,单因素试验方差分析的模型可改写成
![]()
xij可分解成总平均、水平Aj 的效应及随机误差三部分之和,由δj 的定义及单因素测试方差分析的数学模型,显然有
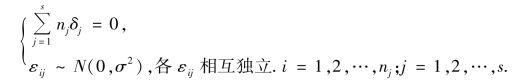
若因素水平的改变不影响总体,即Aj 下总体Xj ~μ(μ+δj,δ2)的均值都相等,则δj(j=1,2,…,s)都等于0.反之,则总有δj 不等于0,因此各水平Aj 对总体的影响可以用效应δj 来表示.从而单因素试验方差分析的假设等价于假设
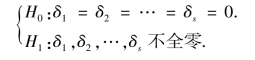
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






