上两节在总体分布形式为已知的前提下，讨论了参数的检验问题.然而在实际问题中，有时不能确知总体服从什么类型的分布，此时就要根据样本来检验关于总体分布的假设.例如检验假设：“总体服从正态分布”等.本节仅介绍χ2 检验法.

所谓χ2 检验法是在总体的分布为未知时，根据样本值x1，x2，…，xn 来检验关于总体分布的假设

的一种方法（这里的备择假设H1 可不必写出）.

注意，若总体X 为离散型，则假设式相当于

若总体X 为连续型，则假设式相当于

在用χ2 检验法检验假设H0 时，若在假设H0 下F（x）的形式已知，而其参数值未知，此时需先用极大似然估计法估计参数，然后再作检验.

χ2 检验法的基本思想与方法如下：

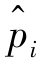①将随机试验可能结果的全体Ω 分为k 个互不相容的事件A1，A2，…，Ak （=Ω，AiAj=ϕ，i≠j；i，j=1，2，…，k），于是在H0 为真时，可以计算概率=P（Ai）（i=1，2，…，k）.

②寻找用于检验的统计量及相应的分布，在n 次试验中，事件Ai 出现的频率与概率往往有差异，但由大数定律可以知道，如果样本容量n 较大（一般要求n 至少为50，最好在100以上），在H0 成立条件下的值应该比较小，基于这种想法，皮尔逊使用

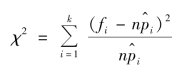
作为检验H0 的统计量，并证明了如下的定理.

定理8.1　若n 充分大（n≥50），则当H0 为真时（不论H0 中的分布属什么分布），统计量χ2 式总是近似地服从自由度为k-r-1 的χ2 分布，其中r 是被估计的参数的个数.

③对于给定的检验水平α，查表确定临界值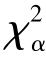（k-r-1）使

从而得到H0 的拒绝域为

④由样本值x1，x2，…，xn 计算χ2 的值，并与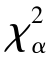（k-r-1）比较.

⑤做判断：若χ2 >（k-r-1），则拒绝H0，即不能认为总体分布函数为F（x）；否则接受H0.

例8.12　一本书的一页中印刷错误的个数X 是一个随机变量，现检查了一本书的100页，记录每页中印刷错误的个数，其结果如表8.5 所示.

表8.5

其中fi 是观察到有i 个错误的页数.问能否认为一页书中的错误个数X 服从泊松分布（取α=0.05）？

解　由题意首先提出假设

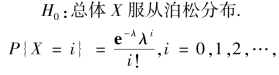
这里H0 中参数λ 为未知，所以需先来估计参数.由最大似然估计法得(www.daowen.com)

将试验结果的全体分为A0，A1，…，A7 两两不相容的事件.若H0 为真，则P{X=i}有估计

例如

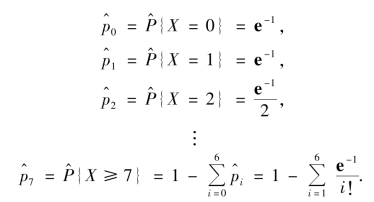
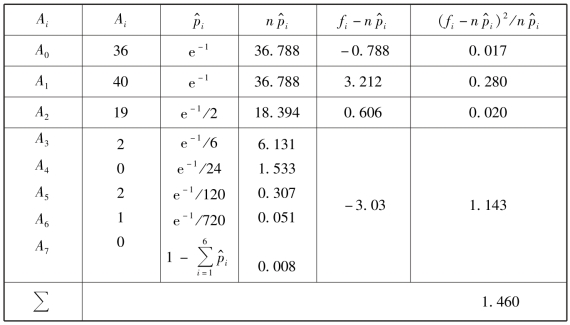
计算结果如表8.6 所示.将其中有些npi <7 的组予以适当合并，使新的每一组内有npi≥7，如表8.6 所示，此处并组后k=4，但因在计算概率时，估计了一个未知参数λ，故

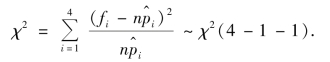
计算结果为χ2=1.460 （表8.6）.因为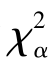（4-1-1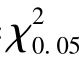）=（2）=5.991 >1.46，所以在显著性水平为0.05 下接受H0，即认为总体服从泊松分布.

表8.6

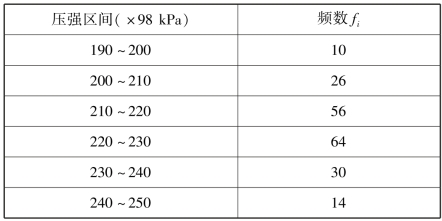
例8.13　研究混凝土抗压强度的分布.200 件混凝土制件的抗压强度以分组形式列出（表8.7）.n==200.要求在给定的检验水平α=0.05 下检验假设

表8.7

解　原假设所定的正态分布的参数是未知的，需先求μ 与σ2 的极大似然估计值.由第7章知，μ 与σ2 的极大似然估计值为

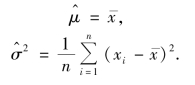
设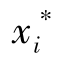为第i 组的组中值，有

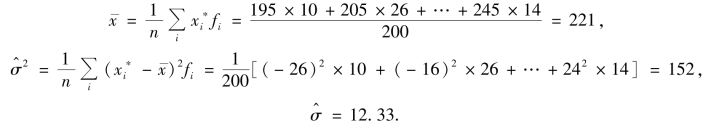
原假设H0 改写成X 是正态N（221，12.332）分布，计算每个区间的理论概率值

其中

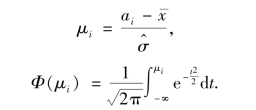
为了计算出统计量χ2 之值，我们把需要进行的计算列表见表8.8.

表8.8

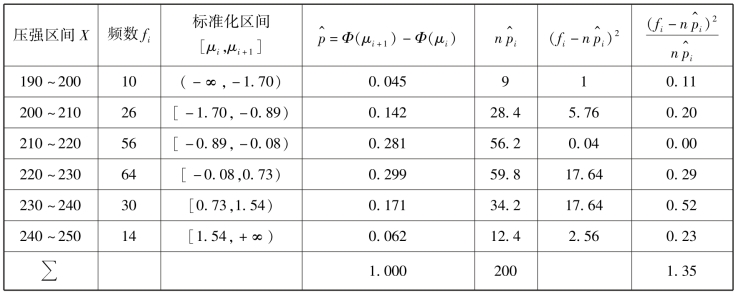
从上面计算得出χ2 的观察值为1.35.在检验水平α=0.05 下，查自由度m=6-2-1=3的χ2 分布表，得到临界值（3）=7.815.因为χ2=1.35 <7.815=（3），不能拒绝原假设，所以认为混凝土制件的抗压强度的分布是正态分布N（221，152）.