【摘要】：为此来检验假设H0：=.解这里n1=n2=10，=0.000 009 56，=0.000 004 89，于是统计量F 的观察值为查F 分布表得由样本观察值算出的F 满足可见它不落入拒绝域，因此不能拒绝原假设H0：=，从而认为两个总体的方差无显著差异.注意：在μ1 与μ2 已知时，要检验假设H0：=，其检验方法类同均值未知的情况，此时所采用的检验统计量是其拒绝域参看表8.4.表8.4单边检验可做类似讨论，限于篇幅，这里不再介绍了.
（1）双边检验
设两正态总体X~N（μ1，
），Y ~N（μ2，
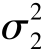），X 与Y 独立，X1，X2，…，Xn1及Y1，Y2，…，
分别是来自这两个总体的样本，且μ1 与μ2 未知.现在要检验假设H0：
=
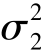.H1：
≠
.
在原假设H0 成立下，两个样本方差的比应该在1 附近随机地摆动，所以这个比不能太大又不能太小.于是我们选取统计量
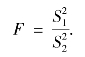
显然，只有当F 接近1 时，才认为有
由于随机变量F∗=
~F（n1-1，n2-1），所以当假设
成立时，统计量
使得
图8.5
由此可知H0 的接受区域是
而H0 的拒绝域为
或(www.daowen.com)
然后，根据样本观察值计算统计量F 的观察值，若F 的观察值落在拒绝域中，则拒绝H0，接受H1.若F 的观察值落在接受域中，则接受H0.
例8.11 在例8.10 中假设两个总体的方差
=
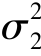，它们是否真的相等呢？为此来检验假设H0：
=
（给定α=0.1）.
解 这里n1=n2=10，
=0.000 009 56，
=0.000 004 89，于是统计量F 的观察值为
查F 分布表得
由样本观察值算出的F 满足
可见它不落入拒绝域，因此不能拒绝原假设H0：
=
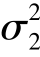，从而认为两个总体的方差无显著差异.
注意：在μ1 与μ2 已知时，要检验假设H0：
=
，其检验方法类同均值未知的情况，此时所采用的检验统计量是
其拒绝域参看表8.4.
表8.4
（2）单边检验
可做类似讨论，限于篇幅，这里不再介绍了.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
