（1）双边检验

设总体X~N（μ，σ2），μ 未知，检验假设

其中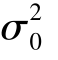为已知常数.

由于样本方差S2 是σ2 的无偏估计，当H0 为真时，比值S2/一般来说应在1 附近摆动，而不应过分大于1 或过分小于1.由第6章知，当H0 为真时

所以对于给定的显著性水平α 有（图8.3）：

对于给定的α，查χ2 分布表可求得χ2 分布分位点

图8.3

由上式知，H0 的接受域是

H0 的拒绝域为

这种用服从χ2 分布的统计量对单个正态总体方差进行假设检验的方法，称为χ2 检验法.

例8.7　某厂生产的某种型号的电池，其寿命（单位：h）长期以来服从方差σ2=5 000 的正态分布，现有一批这种电池，从它们的生产情况来看，寿命的波动性可能有所改变.现随机抽取26 只电池，测出其寿命的样本方差s2=9 200.问根据这一数据是否推断这批电池寿命的波动性较以往有显著水平的变化（取α=0.02）？

解　这是正态总体均值未知时的关于方差的双边假设检验.

①H0:σ2=5 000.H1:σ2≠5 000.

②利用χ2 检验法，选择检验统计量χ2=，H0 为真时，~χ2（25）.

③H0 的拒绝域.给定α=0.02，查表得

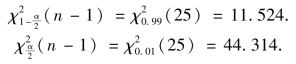
④取样判定χ2==46 >44.314.所以拒绝H0，即可以认为这些电池寿命的波动性较以往有显著的变化.

（2）单边检验（右检验或左检验）

设总体X~N（μ，σ2），μ 未知，检验假设

(www.daowen.com)

由于X~N（μ，σ2），故随机变量

当H0 为真时，统计量

对于显著性水平α （图8.4），有

于是有

可见，当α 很小时，{χ2 >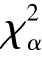（n-1）}是小概率事件，在一次的抽样中认为不可能发生，所以H0的拒绝域为

类似地，可得左检验假设H0：σ2≥，H1：σ2 <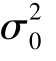的拒绝域为

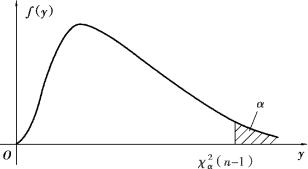
图8.4

例8.8　今进行某项工艺革新，从革新后的产品中抽取25 个零件，测量其直径，计算得样本方差为s2=0.000 66，已知革新前零件直径的方差σ2=0.001 2，设零件直径服从正态分布，问革新后生产的零件直径的方差是否显著减小（取α=0.05）？

⑤做判断：由于χ2=13.2=13.848，即χ2 落入拒绝域中，所以拒绝H0：σ2≥，即认为革新后生产的零件直径的方差小于革新前生产的零件直径的方差.

最后指出，以上讨论的是在均值未知的情况下，对方差的假设检验，这种情况在实际问题中较多.至于在均值已知的情况下，对方差的假设检验，其方法类似，只是所选的统计量为

当σ2=为真时，χ2 ~χ2（n）.

关于单个正态总体的假设检验可见表8.2.

表8.2

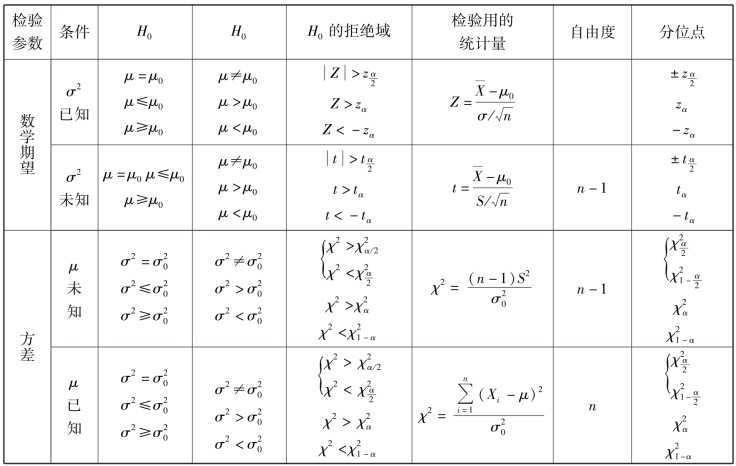
注：上表中H0 中的不等号改成等号，所得的拒绝域不变.