(1)单个正态总体的情形
设正态总体为X,它服从正态分布N(μ,σ2),X1,X2,…,Xn 为来自总体X 的样本.
1)均值μ 的置信区间
①σ2 已知,μ 的置信区间.
引入随机变量U=![]() ,则U~N(0,1).由
,则U~N(0,1).由
![]()
查附表3 得![]() .因此
.因此
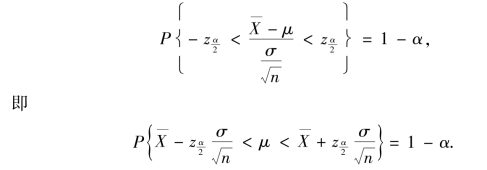

二维码7.3 袋装食品质量问题
故μ 的置信度1-α 的置信区间为
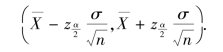
例7.17 已知一批灯泡的使用寿命X 服从正态分布N(μ,302),从中任抽9 只检验,测得它们的平均寿命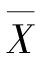 =1 435 h,试求该批灯泡的使用寿命的置信度为0.95 的置信区间.
=1 435 h,试求该批灯泡的使用寿命的置信度为0.95 的置信区间.
解 由题意知,σ=30,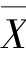 =1 435,n=9,1-α=0.95.选取统计量
=1 435,n=9,1-α=0.95.选取统计量
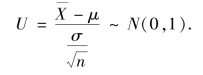
查附表3 得z0.025=1.96,故μ 的置信度为0.95 的置信区间为

即该批灯泡的使用寿命的置信度为0.95 的置信区间(1 415.4,1 454.6).
例7.18 假设参加某种寿险投保人的年龄服从正态分布,标准差σ=7.77 岁.从中抽取36 人组成一个简单随机样本(不重复抽样),其平均年龄为39.5 岁,试建立投保人平均年龄μ的置信度为90%的置信区间.
解 假设用随机变量X 表示某种寿险投保人的年龄,则由已知条件有
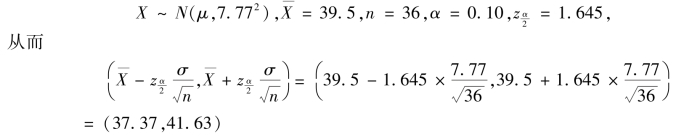
于是可以说有90%的把握确信寿险投保人总体的平均年龄介于(37.37,41.63).
例7.19 2013 年6 月中粮集团对某子公司进行审核,已知发票金额近似服从N(μ,292),现从中抽取100 张作为样本,经过计算样本均值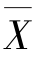 =110.27 元,样本标准差为s=28.95 元,试在95%的置信水平下,求μ 的置信区间.
=110.27 元,样本标准差为s=28.95 元,试在95%的置信水平下,求μ 的置信区间.
解 假设用随机变量X 表示发票金额,则由已知条件有
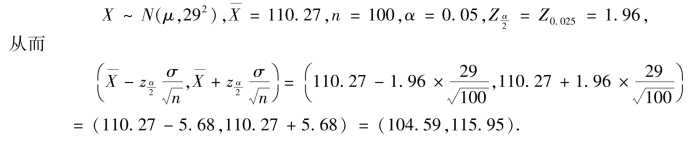
即μ 的置信区间为(104.59,115.95).
②σ2 未知,μ 的置信区间.
引入随机变量
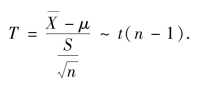
对于给定的α,有
![]()
即
![]()
由
![]()
有
![]()

二维码7.4 新生儿体重估计问题
故μ 的置信度为1-α 的置信区间为
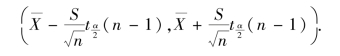
例7.20 从一批钢管中随机抽取10 根,测得其直径尺寸与标准尺寸之间的偏差(单位:mm)分别为
![]()
已知钢管直径尺寸的偏差是一随机变量,记为X,且X ~N(μ,σ2),试求μ 的置信度为1-α=0.90 的置信区间.
解 由题意知,n=10,α=0.1,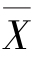 =2,S=
=2,S=![]() ,则
,则
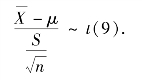
查分位数表得t0.05(n-1)=t0.05(9)=1.833.
因此μ 的置信度为0.90 的置信区间为


二维码7.5 居民服装消费
2)方差σ2 的置信区间
①μ 已知,σ2 的置信区间.
选取统计量
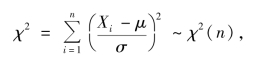
对于给定的α,有

故所求置信区间为
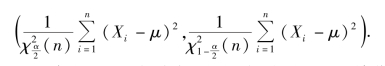
例7.21 某手表厂生产的飞达牌手表,它的走时误差X(单位:s/d)服从正态分布N(0.3,σ2),检验员从装配线上随机地抽取9 只装配好的手表进行测量,得结果如下:
![]()
取置信度为0.95,求这种手表走时误差的方差σ2 的置信区间.
解 由题意可得,μ=0.3,n=9,1-α=0.95.选取统计量
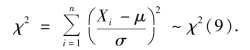
查分位数表得![]()
由样本观测值计算,得
![]()
故手表走时误差σ2 的置信度为0.95 的置信区间为

②μ 未知,σ2 的置信区间.
选取统计量(https://www.daowen.com)

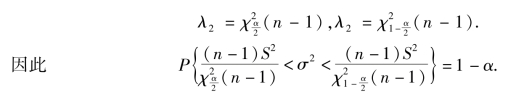
故σ2 的置信度为1-α 的置信区间为

例7.22 分别用金属球测定引力常数(单位:10 -11 m3kg -1s -2),设测定值总体近似服从正态分布N(μ,σ2),μ,σ2 均为未知.金属测定观察值为:
![]()
试在90%的置信水平下,求σ2 的置信区间.
解 由题意得
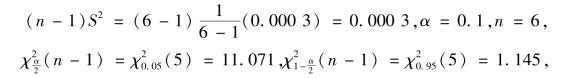
根据公式得,
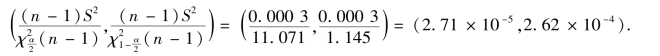
即在90%的置信水平下,σ2 的置信区间为(2.71 ×10 -5,2.62 ×10 -4).
例7.23 假设某厂生产的钢珠直径X(单位:mm)服从正态分布N(μ,σ2),现从该厂刚生产出的一大堆钢珠中随机地抽取9 粒,测量它们的直径,并求得其样本均值 =31.06,样本方差为S2=0.252.试求总体方差的置信度为0.95 的置信区间.
=31.06,样本方差为S2=0.252.试求总体方差的置信度为0.95 的置信区间.
解 由题设条件,可得
![]()
选取统计量
![]()
查分位数表可得![]() (8)=2.18,故σ2 的置信度为0.95 的置信区间为(0.029,0.229).
(8)=2.18,故σ2 的置信度为0.95 的置信区间为(0.029,0.229).
现将正态总体均值与方差的置信区间列于表7.4 中.
表7.4

续表

(2)两个正态总体的情形
设两个正态总体分别为X,Y,它们相互独立且X ~N(μ1,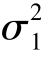 ),Y ~N(μ2,
),Y ~N(μ2, ),X1,X2,…,Xn1和Y1,Y2,…,Yn2分别为来自X 与Y 的样本,
),X1,X2,…,Xn1和Y1,Y2,…,Yn2分别为来自X 与Y 的样本,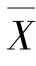 ,
, 分别为X,Y 的样本均值,
分别为X,Y 的样本均值, ,
, 分别为X,Y的样本(修正)方差.
分别为X,Y的样本(修正)方差.
1)两个正态总体的均值差μ1-μ2 的置信区间
① ,
,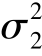 均已知,μ1-μ2 的置信区间.
均已知,μ1-μ2 的置信区间.
选取统计量
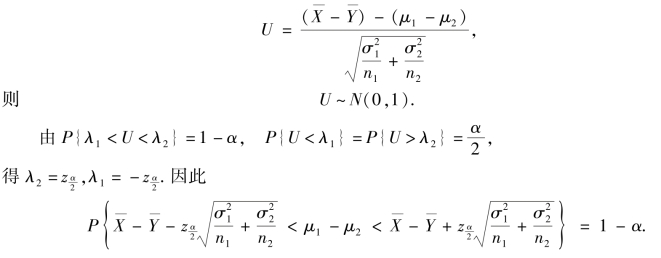
故有μ1-μ2 的置信度为1-α 的置信区间为
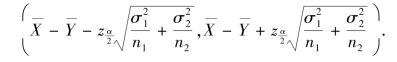
例7.24 某食盐加工厂有甲、乙两条食盐装袋生产线,设所装袋的食盐质量分别服从正态分布N(μ1,52),N(μ2,42).从甲装袋生产线抽取10 袋食盐,测得平均质量 =501 g;从乙装袋生产线抽取20 袋食盐,测得平均质量
=501 g;从乙装袋生产线抽取20 袋食盐,测得平均质量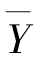 =498 g.取置信度为99%,求甲、乙两条装袋线均值差的置信区间.
=498 g.取置信度为99%,求甲、乙两条装袋线均值差的置信区间.
解 由题设条件可知
![]()
查标准正态分布表得 =2.58.
=2.58.
由于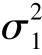 ,
,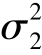 均已知,可得,μ1-μ2 的置信度0.99 的置信区间为
均已知,可得,μ1-μ2 的置信度0.99 的置信区间为


可以推得μ1-μ2 的置信区间为
![]()
例7.25 某公司为了了解男女推销员的推销能力是否有差别,随机抽取16 名男推销员和15 名女推销员进行测试.男推销员的平均销售额为30 250 元,标准差为18 400 元,女推销员的平均销售额为33 750 元,标准差为13 500 元.假设男女推销员的销售额服从正态分布,且方差相等.试建立男女推销员销售额之差的95%的置信区间.
解 假设用随机变量X1,X2 分别表示男女推销员的销售额,则由已知条件有
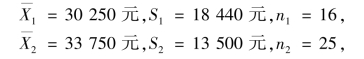
又因两总体方差相等,可以估计出它们的共同方差

与置信度95%相对应的α=0.05,查附表5 得到
![]()
由![]() =σ2,但σ 未知,可得,男女推销员销售额之差的95%的置信区间为
=σ2,但σ 未知,可得,男女推销员销售额之差的95%的置信区间为
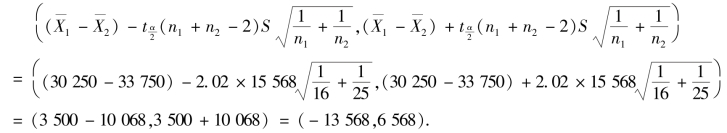
于是,有95%的把握认为男推销员的销售额即有可能比女推销员多6 568 元,也有可能比女推销员少13 568 元,所以男女推销员的推销能力没有显著差别.
例7.26 为了比较甲、乙两类试验田的药材生产的亩产量,现随机地抽取甲类试验田8亩,乙类试验田10 亩,测得亩产量见表7.5.
表7.5

假设这两类实验田的产量X 与Y 相互独立且都服从正态分布,且方差相同.求它们均值之差μ1-μ2 的置信度为0.95 的置信区间.
解 由题设条件,可知
![]()
查分位数表得![]() (n1+n2-2)=t0.025(16)=2.12.
(n1+n2-2)=t0.025(16)=2.12.
由![]() =σ2,但σ 未知,可得μ1-μ2 的置信度0.95 的置信区间为(0.6,2.8).
=σ2,但σ 未知,可得μ1-μ2 的置信度0.95 的置信区间为(0.6,2.8).
2)两个正态总体方差比的置信区间
选取统计量
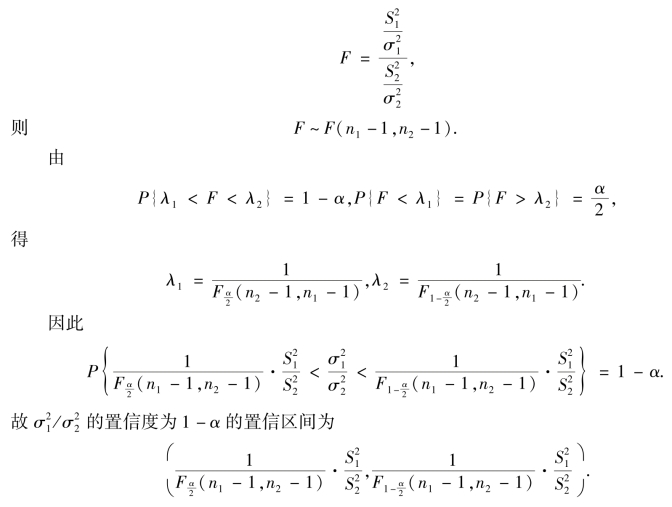
例7.27 为了调查甲、乙两城市地区在1990 年的家庭家计情况,从甲市随机抽出500 户进行调查,得平均每户的年消费支出3 000 元,标准差为400 元.乙市随机抽取1 000 户,调查得平均每户年消费支出4 200 元,标准差500 元.假设甲、乙两城市的每户年消费支出X 和Y都服从正态分布且相互独立,试求甲、乙两城市家庭每户年消费支出方差比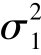 /
/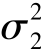 的置信度0.90 的置信区间.
的置信度0.90 的置信区间.
解 由题意知

可得![]() 的置信度0.90 的置信区间为
的置信度0.90 的置信区间为
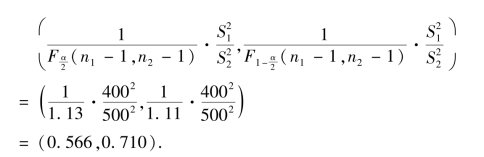
现将两个正态总体均值差和方差比的置信区间列于表7.6 中.
表7.6

表中k=tα(n1+n2-2),Sω=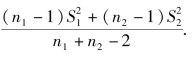
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







