前面介绍了参数的点估计方法，它是用一个统计量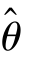作为参数θ 的估计，一旦得到样本的观测值，就能计算出参数的估计值，这种方法方便直观.但它有一个明显的缺陷，就是没有提供估计精确度的任何信息.事实上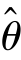， 作为θ 的估计值，与θ 的真实值并不一定相等.很自然地希望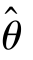落在θ 的真实值的一个很小的邻域内，这便导出了一种新的参数估计的方法，即估计一个很小的邻域，并使这个区间以较大的概率包含参数θ 的真实值，这种估计方法称为区间估计.

定义7.5　设总体X 的分布含有一个未知参数，对于任意给定的数α（0 <α <1），若统计量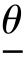（X1，X2，…，Xn）及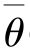（X1，X2，…，Xn）满足

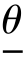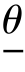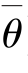则分别称，为参数θ 的置信下限和置信上限，1-α 称为置信度或置信概率（confidence level），区间（ ，）称为置信度1-α 的置信区间（confidence interval）.

定义表明，若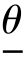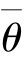（ ，）为参数θ 的置信度1-α 的置信区间，则区间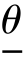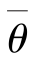（ ，）以概率1-α 包含参数θ 的真值.因此，如果取α=0.05，在进行1 000 次抽样（样本容量保持相同）得到的θ 的1 000 个区间估计中，大约有950 个这样的置信度为（1-α）的置信区间将包含θ 的真值，而每一个具体的置信区间，要么包含θ 的真值，要么不包含θ 的真值.

例7.16　设随机变量X 服从正态分布X ~ N（μ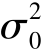，），其中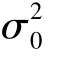为已知，μ 为未知，X1，X2，…，Xn 为来自总体X 的样本，求总体均值μ 的置信度95%的置信区间.

解　由题设，可得

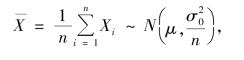
故有

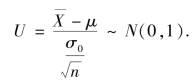
对给定的置信度1-α=95%=0.95，由P{λ1 <U<λ2}=0.95，得

查附表3 得λ1=-1.96，λ2=1.96，即

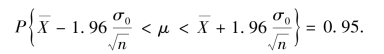(www.daowen.com)

故μ 的置信度95%的置信区间为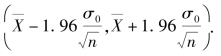

若取P{U>λ2}=0.004，P{U<λ1}=0.001，查附表3 得λ1=-2.33，λ2=1.75，即

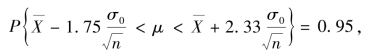
故μ 的置信度95%的置信区间为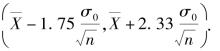

事实上，只要选取λ1，λ2 使P{U<λ1}+P{U>λ2}=0.05，则

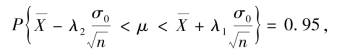
得μ 的置信度95%的置信区间为

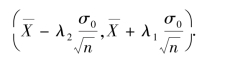
此例说明置信区间不是唯一，有无穷多个.

为统一起见，本书中所涉及的置信度为1-α 的置信区间均是指满足

的区间