【摘要】:对于未知参数θ,如果有两个无偏估计量 与,即E()=E()=θ,那么在, 中谁更好呢?
对于未知参数θ,如果有两个无偏估计量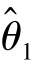 与
与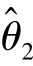 ,即E(
,即E(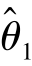 )=E(
)=E(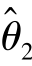 )=θ,那么在
)=θ,那么在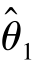 ,
,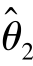 中谁更好呢?此时自然希望
中谁更好呢?此时自然希望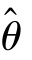 对θ 的平均偏差E[(
对θ 的平均偏差E[(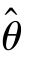 -θ)2]越小越好,即一个好的估计量应该有尽可能小的方差,这就是有效性.
-θ)2]越小越好,即一个好的估计量应该有尽可能小的方差,这就是有效性.
定义7.3 设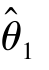 和
和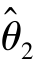 都是未知参数θ 的无偏估计,若对任意的参数θ,有
都是未知参数θ 的无偏估计,若对任意的参数θ,有
则称 比
比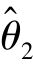 有效.
有效.
如果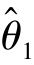 比
比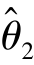 有效,则虽然
有效,则虽然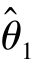 还不是θ 的真值,但
还不是θ 的真值,但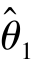 在θ 附近取值的密集程度较
在θ 附近取值的密集程度较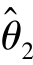 高,即用
高,即用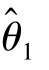 估计θ 精度要高些.
估计θ 精度要高些.
例如,对正态总体X ~ N(μ,σ2),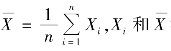 都是E(X)=μ 的无偏估计量,但
都是E(X)=μ 的无偏估计量,但
故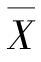 较个别观测值Xi 有效.实际当中也是如此,比如要估计某个班学生的平均成绩,可用两种方法进行估计,一种是在该班任意抽一个同学,就以该同学的成绩作为全班的平均成绩.另一种方法是在该班抽取n 位同学,以这n 个同学的平均成绩作为全班的平均成绩,显然第二种方法比第一种方法好.
较个别观测值Xi 有效.实际当中也是如此,比如要估计某个班学生的平均成绩,可用两种方法进行估计,一种是在该班任意抽一个同学,就以该同学的成绩作为全班的平均成绩.另一种方法是在该班抽取n 位同学,以这n 个同学的平均成绩作为全班的平均成绩,显然第二种方法比第一种方法好.
例7.14 设总体X ~N(μ,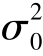 ),其中μ 未知,X1,X2,X3 为X 的一个样本,试证明下列统计量:(https://www.daowen.com)
),其中μ 未知,X1,X2,X3 为X 的一个样本,试证明下列统计量:(https://www.daowen.com)
均为总体参数μ 的无偏估计量,并说明哪一个最有效.
解 因为X1,X2,X3 为X 的一个样本,所以
同理,可得E(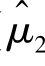 )=μ,E(
)=μ,E(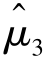 )=μ.
)=μ.
因此μ1,μ2,μ3 均为总体参数μ 的无偏估计量.
又
同理,可得![]() ,故
,故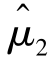 是3 个估计量中最有效的估计量.
是3 个估计量中最有效的估计量.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







