定义7.2　若估计量（X1，X2，…，Xn）的数学期望等于未知参数θ，即

则称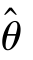为θ 的无偏估计量（non-deviation estimator）.

估计量的值不一定就是θ 的真值，因为它是一个随机变量，若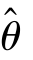是θ 的无偏估计，则尽管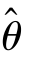的值随样本值的不同而变化，但平均来说它会等于θ 的真值.

例7.12　设X1，X2，…，Xn 为总体X 的一个样本，E（X）=μ，则样本平均数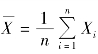是μ 的无偏估计量.

证　因为E（X）=μ，所以E（Xi）=μ，i=1，2，…n，于是

所以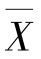是μ 的无偏估计量.

例7.13　设有总体X，E（X）=μ，D（X）=σ2，X1，X2，…，Xn 为从该总体中抽得的一个样本，样本方差S2 及二阶样本中心矩B2=是否为总体方差σ2 的无偏估计？

解　因为E（S2）=σ2，所以S2 是σ2 的一个无偏估计，这也是称S2 为样本方差的理由.由于(www.daowen.com)

且

所以，B2 不是σ2 的一个无偏估计.

在本节开始，提到了例7.8 中θ 的两个估计

因为

由此可以看出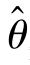矩 是θ 的无偏估计，而L 不是.

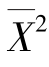一般说来无偏估计量的函数并不是未知参数相应函数的无偏估计量.例如，当X~N（μ，σ2）时，是μ 的无偏估计量，但 不是μ2 的无偏估计量，这是因为