极大似然估计法（maximum likelihood estimation）只是在已知总体分布的前提下进行的一种点估计方法，为了对它的思想有所了解，先看一个例子.

例7.5　假定一个盒子里装有许多大小相同的黑球和白球，并且假定它们的数目之比为3∶1，但不知是白球多还是黑球多，现在有放回地从盒中抽了3 个球，试根据所抽3 个球中黑球的数目确定是白球多还是黑球多.

解　设所抽3 个球中黑球数为X，摸到黑球的概率为p，则X~B（3，p），即

问题是p=还是p=？现根据样本中黑球数，对未知参数p 进行估计.抽样后，共有4种可能结果，其概率如表7.2 所示.

表7.2

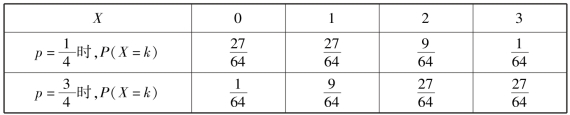
假如某次抽样中，只出现一个黑球，即X=1，p=时，P（X=1）=.p=时，P（X=1）=，会选择p=，即黑球数比白球数为1∶3.因为在一次试验中，事件“1 个黑球”发生了，则认为它应有较大的概率对应着参数p=.同样可以考虑X=0，2，3 的情形，最后可得

由上述例子的估计方法可知，极大似然估计法是要选取这样的θ^，当它作为θ 的估计值时，可以使观察结果出现的可能性最大，即概率最大.

（1）似然函数

在极大似然估计法中，最关键的问题是如何求得似然函数（定义下文给出），有了似然函数，问题就简单了，下面分两种情形来介绍似然函数.

1）离散型总体

设总体X 为离散型，P（X=x）=p（x，θ），其中θ 为待估计的未知参数，假定x1，x2，…，xn 为样本X1，X2，…，Xn 的一组观测值.

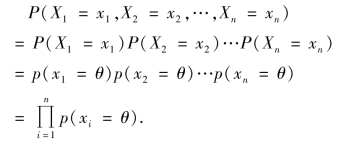
将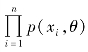看作参数θ 的函数，记为L（θ），即

2）连续型总体

设总体X 为连续型，已知其分布密度函数为f（x，θ），θ 为待估计的未知参数，则样本（X1，X2，…，Xn）的联合密度为

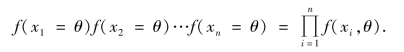
将它也看作关于参数θ 的函数，记为L（θ），即

由此可见，不管是离散型总体，还是连续型总体，只要知道它的概率分布或密度函数，我们总可以得到一个关于参数θ 的函数L（θ），称L（θ）为似然函数.

（2）极大似然估计

极大似然估计法的主要思想：如果随机抽样得到的样本观测值为x1，x2，…，xn，则应当选取未知参数θ 的值使得出现该样本值的可能性最大，即使得似然函数L（θ）取最大值，从而求参数θ 的极大似然估计的问题就转化为求似然函数L（θ）的极值点的问题，一般来说，这个问题可以通过求解下面的方程来解决

然而，L（θ）是n 个函数的连乘积，求导数比较复杂.由于ln L（θ）是L（θ）的单调增函数，所以L（θ）与ln L（θ）在θ 的同一点处取得极大值.于是上述求解方程可转化为求解

称ln L（θ）为对数似然函数，此方程为对数似然方程，求解此方程就可得到参数θ 的估计值.

如果总体X 的分布中含有k 个未知参数θ1，θ2，…，θk，则极大似然估计法也适用.此时，所得的似然函数是关于θ1，θ2，…，θk 的多元函数L（θ1，θ2，…，θk），解下列方程组，就可得到θ1，θ2，…，θk 的估计值，

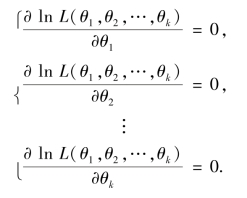
称上述方程组为似然方程组.

例7.6　设总体X 服从0—1 分布，即

设P（A）=p，其中p（0 <p<1）是未知参数，求p 的最大似然估计量.

解　设X1，X2，…，Xn 为总体X 的样本，x1，x2，…，xn 为其观测值，则有

样本似然函数为

两边取对数，得

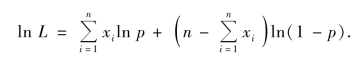
那么，对数似然方程为

解得

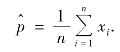
故p 的最大似然估计量为

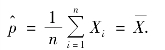
例7.7　若总体X 服从参数为λ 的泊松分布，即

求参数λ 的最大似然估计.

解　设X1，X2，…，Xn 是总体X 的样本，x1，x2，…，xn 是其观测值，则

样本似然函数为

于是(www.daowen.com)

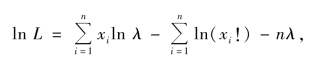
似然方程为

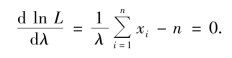
故λ 的最大似然估计为

例7.8　设总体X 服从参数μ，σ2 的正态分布，即X 的概率密度为

X1，X2，…，Xn 为X 的样本，求参数μ，σ2 的最大似然估计.

解　样本的似然函数为

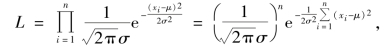
于是

则对数似然方程组为

解方程组，得

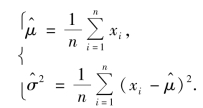
故总体参数μ，σ2 的最大似然估计量为

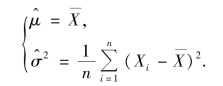
例7.9　设总体X 服从[0，θ]上的均匀分布，X1，X2，…，Xn 是来自X 的样本，求θ 的矩法估计和极大似然估计.

解　因为E（θ）=.令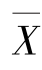=E（X），得

又

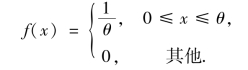
所以

要L（θ）最大，θ 必须尽可能小，又θ≥xi，i=1，2，…，n，从而

例7.10　设总体X 概率密度为

其中α>-1，α 未知，又X1，X2，…，Xn 是来自总体X 的样本，求参数α 的最大似然估计量.

解　样本似然函数为

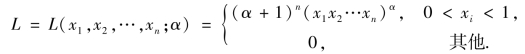
因为0 不是L 的最大值，所以只需考虑

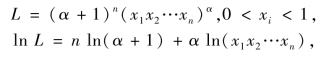
可得对数似然方程为

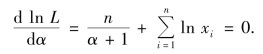
因此，参数α 的似然估计量为

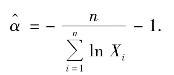
例7.11　某公司出售某款手机，需要知道它的平均使用寿命.设该款手机寿命X 服从参数为θ 的指数分布.现对7 只该款手机的使用寿命进行跟踪调查，得到的数据见表7.3.

表7.3

用极大似然估计法估计手机的平均使用寿命.

解　设手机的寿命为X，则X 的密度函数为

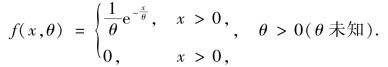
设X1，X2，…，Xn 为总体X 的样本，x1，x2，…，xn 为其观测值，则样本的似然函数为

两边取对数，得

似然方程为

解得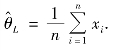

把样本值代入极大似然估计量，得到=2.5，即手机的平均寿命是2.5 年.

二维码7.2　基因问题