定理6.1　设X1，X2，…，Xn 来自正态总体X~N（μ，σ2）的一个简单样本，则对于样本均值

定理6.2设总体X服从正态分布N（μ，σ2），（X1，X2，…，Xn）为来自总体X 的一个样本，分别表示样本均值与样本（修正）方差，则有

定理6.3　设X~N（μ，σ2），（X1，X2，…，Xn）为来自总体X 的样本，则随机变量

服从自由度为n-1 的t 分布，即T~t（n-1）.

证　由条件可得，因此

又因为

且X 与S2 相互独立，于是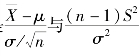亦相互独立，故

定理6.4　设（X1，X2，…，Xm）（m≥2）和（Y1，Y2，…，Yn）（n≥2）分别是总体X~N（μ1，σ2）和Y~N（μ2，σ2）的两个相互独立的简单随机样本，则(www.daowen.com)

且由条件可知它们相互独立，所以由χ2 分布的性质得

本节所介绍的三个分布以及四个定理，在下面各章中都起着重要的作用.应注意，它们都是在总体为正态总体这一基本假定下得到的.

例6.4　设X1，X2，…，Xn 为来自总体N（μ，σ2）（σ >0） 的简单随机样本，记统计量T=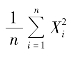，求E（T）.

例6.5　设总体X 服从正态分布N（62，100），为使样本均值大于60 的概率不小于0.95，问样本容量n 至少应取多大？

解　设需要样本容量为n，则

查标准正态分布表，得Φ（1.64）≈0.95.所以

故样本容量至少应取68.