统计量是样本的函数，它是一个随机变量.统计量的分布称为抽样分布.在使用统计量进行统计推断时常需知道它的分布.当总体的分布函数已知时，抽样分布是确定的，然而要求出统计量的精确分布，一般来说是困难的.本节介绍来自正态总体的几个常用的统计量的分布.

（1）χ2 分布

定义6.5　设X1，X2，…，Xn 是独立同分布的来自总体N（0，1）的样本，则统计量

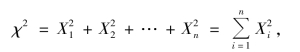
所服从的分布称为自由度为n 的χ2 分布（χ2-distribution），记作χ2 ~χ2（n）.

χ2（n）分布的概率密度函数为

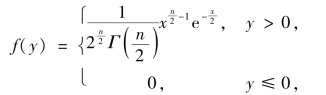
其中，Γ（r）=

χ2 分布具有以下性质：

①密度函数非负，且E（χ2）=n，D（χ2）=2n.

②可加性：若X~χ2（n1），Y~χ2（n2），且X 与Y 独立，则X+Y~χ2（n1+n2）.

定义6.6　设随机变量X~χ2（n），对任意给定的实数α（0 <α<1），称满足P{X >λ}=α的实数λ 为自由度为n 的χ2 分布的α 水平上侧分位数，记为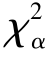（n），即λ=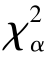（n）.

由定义6.5 可知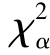，（n）不仅与n 有关，还与α 有关，如图6.1 所示.

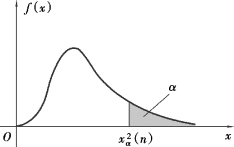
图6.1

χ2 分布的上侧分位数表见书后附表4.值得注意的是，在χ2 分布的上侧分位数表中，一般仅对n≤45 给出了分位数的值，当n>45 时，不加证明地给出如下的近似公式，即

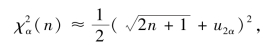
其中u2α由Φ（u2α）=1-α 查标准正态分布表得出.

例6.1　已知随机变量X~χ2（25），求满足下列各式的实数λ 的值：

①P{X>λ}=0.01.

②P{X<λ}=0.025.

③P{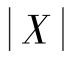>λ}=0.05.

解　因为X~χ2（25），

（1）由P{X>λ}=0.01，所以λ=（25），查χ2 分布的分位数表知（25）=44.314，所以λ=44.314.

（2）由P{X<λ}=0.025，得P{X >λ}=0.975，λ=（25），查χ2 分布的分位数表知（25）=13.120，所以λ=13.120.

（3）由=0.05，得P{X >λ}=0.005，查χ2 分布的分位数表知（25）=37.652，所以λ=37.652.

（2）t 分布

定义6.7　设随机变量X ~N（0，1），Y ~χ2（n），且X 与Y 相对独立，则称随机变量t=服从自由度为n 的t 分布（t-distribution），记作t~t（n），其概率密度函数为

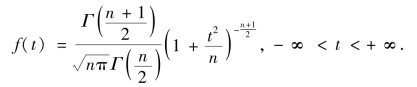
t 分布具有以下的性质：

①t 分布是对称分布，且为低峰分布，当n→∞时，极限分布为X~N（0，1）.

②当n>1 时，E（t）=0.当n>2 时，D（t）=

定义6.8　若随机变量X~t（n），对于任意给定的数α（0 <α <1），称由=α所确定的实数λ 为自由度为n 的t 分布的α 水平双侧分位数，记作tα（n），即λ=tα（n）.

由定义6.7 可得，若λ 为自由度为n 的t 分布的α 水平双侧分位数，则

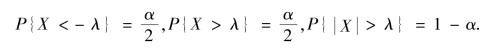(www.daowen.com)

图6.2 所示是t 分布的双侧分位数图.t 分布的双侧分位数表见附表5.

对于t（n）分布的α 分位数有tα（n）=-t1-α（n）.当n>60 时，有近似公式

其中uα 由Φ（uα）=1-查标准正态分布表得出.

例6.2　已知随机变量X~t（12），求满足下列各式的实数λ 的值：

①P=0.001.

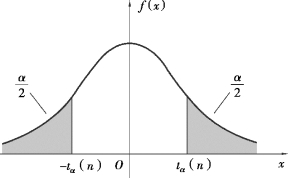
图6.2

②P{X<λ}=0.975.

③P{X>λ}=0.01.

解　因为X~t（12），

①由P{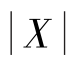>λ}=0.001，得λ=t0.001（12），查t 分布的分位数表知t0.001（12）=4.318，所以λ=4.318.

②由P{X<λ}=0.975，得P{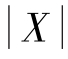>λ}=0.05，λ=t0.05（12），查t 分布的分位数表知t0.05（12）=2.179，所以λ=2.179.

③由P{X >λ}=0.01，得P{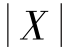>λ}=0.02，λ=t0.02（12），查t 分布的分位数表知t0.02（12）=2.681，所以λ=2.681.

（3）F 分布

定义6.9　设随机变量X~χ2（m），Y~χ2（n），且X 与Y 相互独立，则称随机变量F=服从自由度是（m，n）的F 分布（F-distribution），记为

其中m 称为第一自由度，n 称为第二自由度，其概率密度函数为

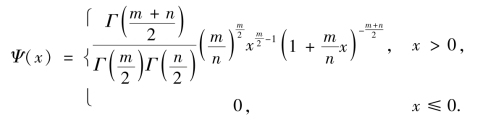
F 分布具有下面的性质：

①密度函数在正半轴非负.

②F~F（m，n），则~F（n，m）.

定义6.10　设随机变量X~F（m，n），对于任意给定的数α（0 <α<1），称由P {X>λ}=α所确定的实数λ 为自由度为m 和n 的F 分布的α 水平上侧分位数，记作Fα（m，n），即λ=Fα（m，n）.

对于F（m，n）分布的α 分位数有Fα（m，n）=

图6.3 所示是F 分布的上侧分位数图.F 分布的上侧分位数见附表6.

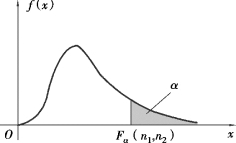
图6.3

例6.3　已知随机变量X~F（10，15），求满足下列各式的实数λ 的值：

①P{X>λ}=0.01.

②P{X<λ}=0.975.

解　因为X~F（10，15），那么

①由P{X >λ}=0.01，得λ=F0.001（10，15），查F 分布的分位数表知F0.001（10，15）=3.80，所以λ=3.80.

②由P{X<λ}=0.975，得P{X>λ}=0.025，λ=F0.025（10，15），查F 分布的分位数表知F0.025（10，15）=3.06，所以λ=3.06.