（1）统计量的定义

样本是总体的反映，但是由于样本所含的信息比较分散，不能直接用于解决我们所要研究的问题，为使这些分散的信息集中起来反映总体的某些特征，需要把样本所含的信息进行数学上的加工而使其浓缩起来，一种有效的方法就是构造样本的函数.不同的样本函数反映总体不同的特征.这样的函数称为统计量.

定义6.4　设（X1，X2，…，Xn）为取自总体X 的一个样本，g（X1，X2，…，Xn）为X1，X2，…，Xn的一个实值函数，且g（X1，X2，…，Xn）中不包含任何未知参数，则称g（X1，X2，…，Xn）为一个统计量（statistic）.

注：“不含任何未知参数”是强调在获得了样本的观测值（x1，x2，…，xn）后，带入统计量即可以得到统计量的观测值g（x1，x2，…，xn）.

（2）常用统计量

下面我们定义一些常用的统计量，设（X1，X2，…，Xn）是来自总体X 的一个样本；（Y1，Y2，…，Yn）是来自总体Y 的一个样本.

1）样本均值

对于简单随机样本，由于样本中的数据有大有小，而样本均值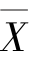总处于样本的中间位置，即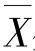处于取值范围的中心，那么样本均值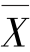将是总体均值的一个很好的估计量，是反映总体分布均值所在位置信息的一个统计量.例如，总体均值是μ，则样本均值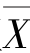将是μ 的一个很好的估计量.(www.daowen.com)

2）样本（修正）方差

3）样本（未修正）方差

4）样本标准差

5）样本k 阶原点矩

6）样本k 阶中心矩

将统计量中的Xi 替换为观察值xi 即可得到统计量的观察值.