定理5.2（切比雪夫大数定律）　设X1，X2，…，Xn，…是相互独立的随机变量序列，E（Xi），D（Xi）（i=1，2，…）都存在，且存在C>0，使得D（Xi）≤C（i=1，2，…），则对任意的ε>0，有

切比雪夫大数定律表明，当n 充分大时，n 个相互独立的随机变量的平均值以较大的概率聚集在其数学期望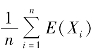的附近.这就从理论上证明了，独立随机变量的平均值具有稳定性.

推论1　设独立随机变量序列X1，X2，…，Xn，…具有相同的数学期望与方差，且E（Xi）=μ，D（Xi）=σ2（i=1，2，…），则对任意的ε>0，有

二维码5.1　评委打分问题

定理5.3（伯努利大数定律）　设X 是n 重贝努里试验中事件A 发生的次数，p（0 <p<1）是事件A 在每次试验中发生的概率，则对于任意的ε>0，有

或

证　记Xi=“第i 次试验中事件A 发生的次数”，i=1，2，…，n，则由条件可知，Xi 是离散型随机变量，且

则X=X1+X2+…+Xn，其中X1，X2，…，Xn 是n 个相互独立的随机变量，

由于

由切比雪夫不等式有(www.daowen.com)

因为

所以

而

故有

由伯努利大数定理我们知道，事件发生的频率依概率收敛于事件的概率.这个定理以严格的数学形式证明了频率的稳定性，揭示了独立重复试验中频率“靠近”概率这一客观现象，它是概率论的理论基础.伯努利大数定律和切比雪夫大数定律都要求随机变量的方差存在，下面介绍独立同分布的辛钦大数定律，从中可见，方差存在这一条件并不是必要的.

定理5.4（辛钦大数定律）　设X1，X2，…，Xn，…为独立同分布的随机变量序列，E（Xi）=μ（i=1，2，…），则对任意的ε>0，有

或

证　证明超出本书的范围，略.

辛钦（Khinchin）大数定律表明，只要独立同分布的随机变量序列的数学期望存在，当n 充分大时，随机变量X 在n 次重复独立观测中的算术平均值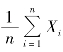，以较大的概率聚集于E（X）附近，这就为随机变量X 的数学期望的估计提供了一条可行的途径，为数理统计中“参数估计” 提供了理论依据.