定理5.1（切比雪夫不等式）　设随机变量X 存在有限方差D（X），则对任意ε>0，有

证　如果X 是连续型随机变量，设X 的概率密度函数为f（x），则有

请读者自己证明离散型随机变量的情况.

切比雪夫不等式也可表示为

从切比雪夫不等式可以看出，随机变量X 的方差较小，则X 的取值越集中在其“中心”E（X）的附近.方差较小，X 取值在区间（E（X）-ε，E（X）+ε）外的概率越小，即越集中在区间（E（X）-ε，E（X）+ε）内.这也表明D（X）的大小体现了X 取值的分散程度.以后还将会看到，这个不等式还是大数定律的理论基础.

例5.1　将一颗骰子连续重复抛掷4 次，以X 表示4 次掷出的点子数之和，则根据切比雪夫不等式，说明P{10 <X<18}应不小于多少？

解　以Xk（k=1，2，3，4）分别表示第k 次掷出的点数，则Xk 独立且服从相同的分布.

又由于X=X1+X2+X3+X4，而X1，X2，X3，X4 相互独立，所以

因此，根据切比雪夫不等式，有

故P{10 <X<18}应不小于多少

例5.2　设电站供电所有10 000 盏电灯，夜晚每一盏灯开灯的概率都是0.7，而假定开关时间彼此独立，估计夜晚同时开着的灯数在6 800 盏与7 200 盏之间的概率.

解　令X 为同时开灯的数目，则X~B（10 000，0.7）.

上式的计算较为烦琐，我们可利用切比雪夫不等式进行估计.

可见，虽然有10 000 盏灯，但是只要有供应7 200 盏灯的电力就能够以相当大的概率保证够用.事实上，切比雪夫不等式的估计只说明概率大于0.95，后面将具体求出这个概率约为0.999 99.切比雪夫不等式在理论上具有重大意义，但作为对概率值的估计的精确度不高.切比雪夫不等式作为一个理论工具，在大数定律的证明中，可使证明非常简洁.(www.daowen.com)

例5.3（白细胞估计问题）　已知正常男性成人血液中，每1 mL 白细胞平均是7 300，均方差是700.试估计每1 mL 白细胞数在（5 200，9 400）之外的概率.

解　记X 为正常男性血液每1 mL 白细胞数，由题意知

应用切比雪夫不等式，得到

人们在长期的实践中发现，事件发生的频率具有稳定性.也就是说，随着试验次数的增多，事件发生的频率稳定于一个确定的常数.另外，人们在长期的生产实践活动中还认识到，不但事件的频率具有稳定性，而且大量随机现象的结果的平均值也具有稳定性.大数定律正是以数学形式明确表达，并证明了在相同条件下大量随机试验的这一规律.

定义5.1　设X1，X2，…，Xn，…是一个随机变量序列，如果存在一个随机变量（或常数）X，使得对任意给定的ε>0，有

或

则称随机变量序列X1，X2，…，Xn，…依概率收敛于X，记作

值得注意的是，在定义5.1 中X 既可以是随机变量，也可以是某个常数，在后面的应用中，X 均为常数.

定义5.2　设X1，X2，…，Xn，…为一随机变量序列，且Xi（i=1，2，…）的数学期望存在，若对任意给定的ε>0，有

或

则称随机变量序列X1，X2，…，Xn，…服从大数定律.

从上述定义可知，在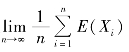收敛的条件下，随机变量序列X1，X2，…，Xn，… 服从大数定律与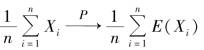等价.