【摘要】：协方差的数值在一定程度上反映了X 与Y 间的相互关系，但它还受X 与Y 本身数值大小的影响.比如说，令X 与Y 各自增大k 倍，即X1=kX，Y1=kY，这时X1 与Y1 间的相互关系和X与Y 间的相互关系应该是一样的，可它们的协方差却增大了k2 倍，即有为了克服这一问题，引入相关系数这一概念.定义4.5设X 与Y 是两个随机变量，D（X） >0，D（Y） >0，则称为X 与Y 的相关系数（co
为了检验线性回归直线是否显著，还可用x 与y 之间的相关系数来检验.相关系数的定义是
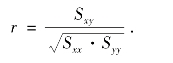
由于
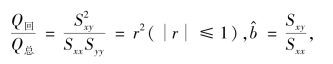
则
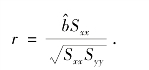
显然r 和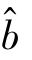
的符号是一致的，它的值反映了x 与y 的内在联系.
提出检验假设
可以证明，当H0 为真时，
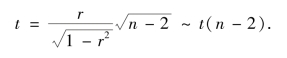
故H0 的拒绝域为
(www.daowen.com)
由上例的数据可算出
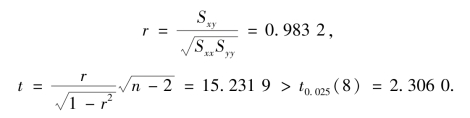
故拒绝H0，即两变量的线性相关性显著.
在一元线性回归预测中，相关系数检验与F 检验法等价，在实际中只需作其中一种检验即可.
与一元线性回归显著性检验原理相同，为考察多元线性回归这一假定是否符合实际观察结果，还需进行以下假设检验：
可以证明统计量
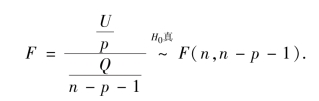
其中
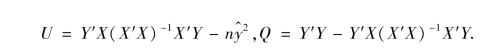
给定水平α，若F≥Fα，则拒绝H0，即认为回归效果是显著的.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
