定义4.4　设（X，Y）为二维随机变量，称E[（X-E（X））（Y-E（Y））]为随机变量X 与Y的协方差（covariance），记为cov（X，Y），即

由数学期望的性质，从上式不难得出

此式更适用于协方差的计算.特别地，

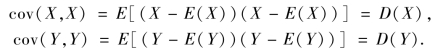
故方差D（X），D（Y）是协方差的特例.

对于离散型随机变量X 与Y，协方差的计算公式可化为

其中pij是（X，Y）的联合概率函数.

对于连续型随机变量X 与Y，协方差的计算可化为

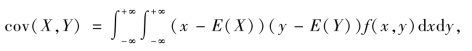
其中f（x，y）是（X，Y）的联合概率密度函数.

例4.17　袋中装有标上号码1，2，2 的3 个球，从中任取一个并且不再放回，然后再从袋中任取一球，以X，Y 分别记为第一，二次取到球上的号码数，求X 与Y 的协方差.

解　可以求出X 与Y 的联合分布律见表4.12.

表4.12

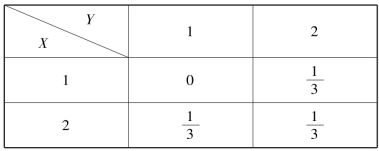
由于对称性，X 与Y 的边缘分布律相同，即

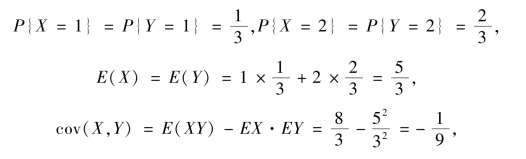
则

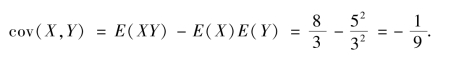
例4.18　箱内有6 个球，其中红，白，黑球的个数分别为1，2，3.现在从箱中随机的取出2个球，设X 为取出的红球个数，Y 为取出的白球个数，

①求随机变量（X，Y）的联合分布律.

②求cov（X，Y）.

解　①由题意知，X 的可能取值为0，1.Y 的可能取值为0，1，2.(www.daowen.com)

经计算得（X，Y）的联合分布律见表4.13.

表4.13

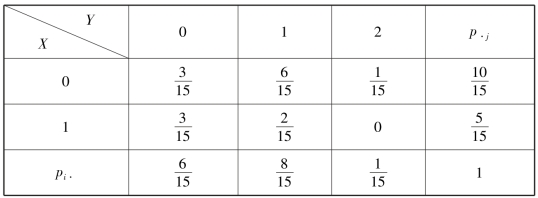
②由定义有，E（X）=0 ×，

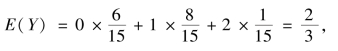
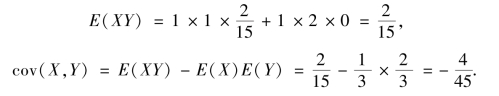
例4.19　设（X，Y）的概率密度为

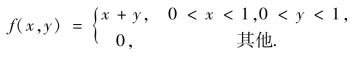
求cov（X，Y）.

解　由于

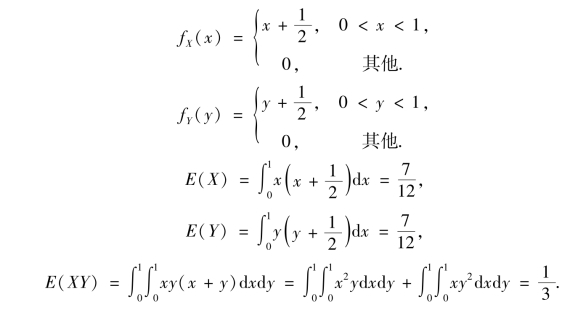
因此

由协方差的定义知，它具有以下性质.

性质1　若X 与Y 相互独立，则cov（X，Y）=0.

性质2　cov（X，Y）=cov（Y，X）.

性质3　若a，b 为两个任意常数，则cov（aX，bY）=ab cov（X，Y）.

性质4　cov（X1+X2，Y）=cov（X1，Y）+cov（X2，Y）.

性质5　D（X±Y）=D（X）+D（Y） ±2 cov（X，Y）.

证　D（X±Y）=E[（X±Y）-E（X±Y）]2

　　　　=E[(X-E(X))2 ±2(X-E(X))(Y-E(Y))+(Y-E(Y))2]

　　　　=E(X-E(X))2 ±2E[(X-E(X))(Y-E(Y))]+E(Y-E(Y))2

　　　　=D(X)+D(Y) ±2cov(X,Y).