方差有下面几条重要的性质.

设随机变量X 与Y 的方差存在，则

性质1　设C 为常数，则D（C）=0.

性质2　设a 为常数，则D（aX+b）=a2D（X）.

性质3　D（X±Y）=D（X）+D（Y） ±2E{[X-E（X）][Y-E（Y）]}.

性质4　若X，Y 相互独立，则D（X±Y）=D（X）+D（Y）.

性质5　若X1，X2，…，Xn 相互独立，则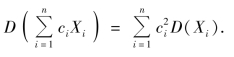

证　对性质1，由E（C）=C 有

对性质2，即

对性质3，即

其中，由于X，Y 相互独立，X-E（X）与Y-E（Y）也相互独立，由数学期望性质4 知

即得(www.daowen.com)

这一性质可以推广到任意有限多个相互独立的随机变量之和（差）的情况.

例4.14　设两个相互独立的随机变量X 和Y 的方差分别为4 和2，求随机变量3X-2Y 的方差.

解　由于X 和Y 相互独立，故由方差的性质，有

例4.15　设随机变量X 的数学期望为E（X），方差D（X）=σ2（σ >0），令X∗=

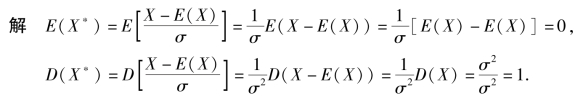
称X∗为X 的标准化随机变量.

例4.16　设活塞的直径（以cm 计）X ~ N（22.40，0.032），汽缸的直径Y ~ N（22.50，0.042），X，Y 相互独立，任取一只活塞，任取一只汽缸，求活塞能装入汽缸的概率.

解　依题意需求P（X<Y）=P{X-Y<0}.

令Z=X-Y，则

即Z~N（-0.10，0.052），

故有