性质1　设c 是常数，则E（c）=c.

性质2　设X 是随机变量，c 是常数，则E（cX）=cE（X）.

性质3　设X，Y 是任意两个随机变量，则E（X+Y）=E（X）+E（Y）.

证　就离散型的随机变量证明如下（连续型的情况请读者自己试证）.

设X 和Y 是离散型随机变量，pij是二维随机向量（X，Y）的联合分布律，其边缘分布是pi·和p·j，于是

性质3 可推广到任意有限个随机变量的情况，即

不难看出

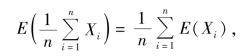
即n 个随机变量的算术平均值的期望等于这n 个随机变量期望的算术平均数.

性质4　设X，Y 是两个相互独立的随机变量，则有

证　就连续型的随机变量证明.

设X，Y 是连续型随机变量，f（x，y）是二维连续型随机向量的联合概率密度函数，fX（x）与fY（y）分别是X 与Y 的边缘密度函数.

由于X，Y 独立，则有f（x，y）=fX（x）fY（y）.

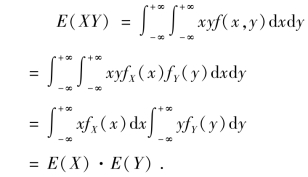
必须注意此性质中的X 与Y 是相互独立的随机变量.性质4 可以推广到任意有限个相互独立的随机变量之积的情况.

例4.7（血液分组检测问题）　某地区共有100 人参加疾病普查，已知每人血液呈阳性的概率是0.1，现采取两种方案进行血液化验.

方案一：逐一进行化验.

方案二：每10 人为一组进行化验.

问哪种方案最优？

解　易知采用第一种方案需100 次.

现讨论第二种方案.(www.daowen.com)

记随机变量X 为一组需要检验的次数，X 的可能性取值为：1，11，且

故得X 的分布律见表4.7.

表4.7

每组所需的平均检验次数

方案二总检验次数：Z=X1+X2+…+X10，由于Xi 与X 同分布，所以

通过比较可得到，方案二优于方案一.

例4.8　设一电路中电流I（A）与电阻R（Ω）是两个相互独立的随机变量，其概率密度函数分别为

试求电压V=IR 的均值.

解　E（V）=E（IR）=E（I）E（R）

例4.9　某一民航送客的车载有20 位旅客自机场开出，旅客有10 个车站可以下车，但如到达一个车站没有人下车就不停车.假设每位旅客在各个车站下车是等可能的，并设各个旅客是否下车是相互独立.求停车次数的数学期望.

解　令X 为停车次数，并设

显然X=X1+X2+…+X10，下面来求E（X）.

由题意，任一旅客在第i 站不下车的概率为，因此20 位旅客都不在第i 站下车的概率为，因而有

因此得