【摘要】:定理4.1设Y 是随机变量X 的函数Y=g①X 是离散型随机变量,它的分布律为P{X=xi}=pi,i=1,2,…
定理4.1(随机变量函数的数学期望) 设Y 是随机变量X 的函数Y=g(X)(g 是连续函数)
①X 是离散型随机变量,它的分布律为P{X=xi}=pi,i=1,2,…,若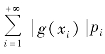 收敛,则有
收敛,则有

②X 是连续型随机变量,它的概率密度为f(x),若![]() 收敛,则有
收敛,则有
![]()
定理4.1 的重要意义在于,当我们求E(Y)时,不必知道Y 的分布而只需知道X 的分布就可以了.当然,我们也可以由已知的X 的分布,先求出其函数g(X)的分布,再根据数学期望的定义去求E[g(X)].然而,有时候Y=g(X)的分布是不容易求出的,所以一般不采用后一种方法.
定理4.1 的证明超出了本书的范围,这里不予证明.
定理4.2 设Z 是随机变量X,Y 的函数,则Z=g(X,Y)(g 是连续函数).
①若(X,Y)为离散型随机变量,其分布律为P{X=xi,Y=yj}=pij,i,j=1,2,…,则有
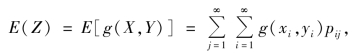
这里设上式右边的级数绝对收敛.
②若(X,Y)为连续型随机变量,其联合概率密度为f(x,y),则有
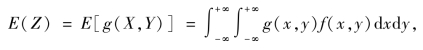
这里设上式右边的积分绝对收敛.
特别地,设(X,Y)是二维连续型随机变量,其概率密度函数为f(x,y),则(https://www.daowen.com)
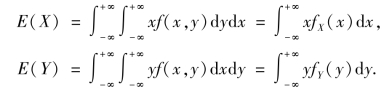
例4.5 设随机变量X 的分布律如表4.6 所示.
表4.6

求E(X2),E(-2X+1).
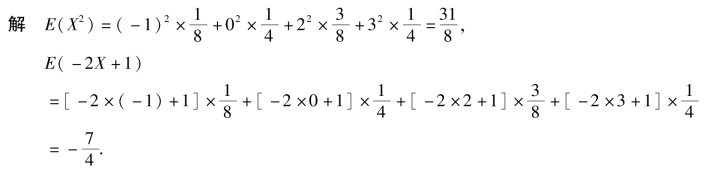
例4.6 设X~N(1,4),

求E(Y).
解 方法一:直接根据随机变量的函数求期望的公式求解.
设X 的密度函数为f(x),则
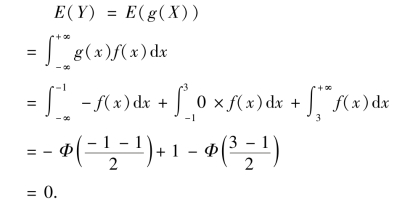
方法二:先求出Y 的分布列
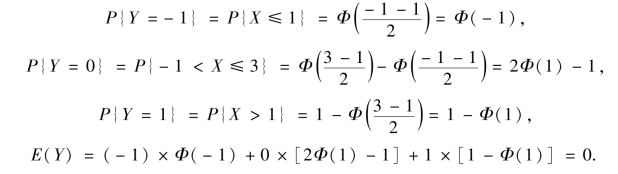
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章








