(1)数学期望的定义
设随机变量X 的分布律为P(X=xi)=pi,i=1,2,…,我们希望能找到这样一个数值(仅仅是“一个数值”),它体现了X 取值的平均大小,就如同通常一组数字的平均数那样.在引入数学期望的概念之前,先看一个例子.
对于一组数,比如-1.1,1.9,0.2,0.5,0.5,它们的平均数是
![]()
可是,对一个随机变量X 而言,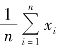 只是一种算术平均,并不能真正起到平均的作用.
只是一种算术平均,并不能真正起到平均的作用.
例如,若X 的分布律如表4.1 所示X 取值的平均数是150,但150 并不能真正体现X 的真实均值,这是因为错误的认为X 取100与200 的概率是一样的.但实际上,从分布看来,X 取200 比取100 的概率大得多,因此要体现X 的真实均值,不能只由它取什么值来决定,必须考虑到它取那些值对应的概率.
表4.1

定义4.1 设离散型随机变量X 的分布律为P{X=xi}=pi,i=1,2,….若正项级数![]() 绝对收敛,则称之为随机变量X 的数学期望(mathematical expectation),以下简称期望,记作E(X).即
绝对收敛,则称之为随机变量X 的数学期望(mathematical expectation),以下简称期望,记作E(X).即
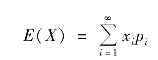

二维码4.1 赌金分配问题
注 定义中要求该级数绝对收敛,是为了保证该级数的值不受求和过程中各项次序的影响.
显然,E(X)是一个实数.它形式上是随机变量X 的取值以概率为权的加权平均值,实质上它体现了随机变量X 取值的真正平均.为此,我们也称它为X 的均值.
对于上面提到的那个例子,就有E(X)=100 ×0.01+200 ×0.99=199,它与200 非常靠近,而远不是150.
例4.1(经济决策问题) 某企业需要是否与一家外企联营做出决策,经过调查做出评估,联营成功的概率为0.35,若联营成功可增加利润50 万元/月.若联营失败将损失20 万元/月.若不联营利润不变,企业该如何决策?
解 用X 表示选择联营能增加的利润值,则X 的概率分布为
![]()
所以,选择联营能增肌的利润期望值为
![]()
若不联营,该企业增加的利润为0.
因此,该企业应该作出联营的决策.
例4.2 设某车站每天8:00—9:00,9:00—10:00 都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间相互独立,其规律见表4.2.
表4.2

①有一旅客8:00 到车站,求他候车时间的数学期望;
②有一旅客8:20 到车站,求他候车时间的数学期望.
解 设旅客的候车时间为X 分布律.
①由题意可知,X 的分布律见表4.3.(https://www.daowen.com)
表4.3

则

②由题意可知,X 的分布律见表4.4.
表4.4

上表中概率的计算说明,如P{X=70}=P{AB}=P(A)P(B)=![]() ,A=“第一班车在8:10 到站”,B=“第二班车在9:30 到站”.则
,A=“第一班车在8:10 到站”,B=“第二班车在9:30 到站”.则
![]()
(2)常用离散型分布的数学期望
1)0—1 分布
设X 服从参数为p 的0—1 分布(p>0),其概率函数见表4.5.
表4.5

由期望的定义公式计算得
![]()
2)二项分布
设X~B(n,p),其概率函数为
![]()
由期望的定义公式计算得
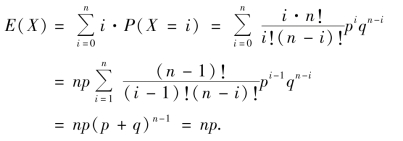
3)泊松分布
设X 服从参数为λ 的泊松分布,其分布律为
![]()

二维码4.2 求职面试问题
由期望的定义公式计算得
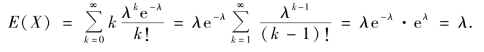
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





