设(X,Y)为二维连续型随机向量,它们的联合概率密度为f(x,y),令g(x,y)是二元函数,则g(X,Y)是(X,Y)的函数.可以用求一元随机变量函数分布的方法,求Z=g(X,Y)的分布.首先求分布函数

二维码3.2 食堂窗口规划问题
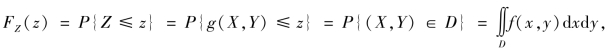
其中,D={(x,y) g(x,y)≤z}.对几乎所有的z,有Z 的概率密度为
g(x,y)≤z}.对几乎所有的z,有Z 的概率密度为
![]()
一般,我们有如下定理.
定理3.7 设f(x1,x2)是连续型随机向量(X1,X2)的联合概率密度,如果函数y1=g1(x1,x2),y2=g2(x1,x2)满足下列条件
①存在唯一的反函数x1=h1(y1,y2),x2=h2(y1,y2).
②反函数存在连续的偏导数.
③反函数的雅可比(Jacobi)行列式
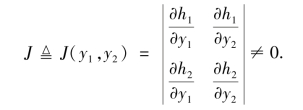
则Y1,Y2 的联合概率密度(Y1=g1(X1,X2),Y2=g2(X1,X2)),为
![]()
证 设W(y1,y2)为(y1,y2)的联合分布函数,则对任意的实数有
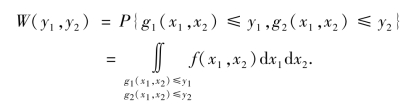
令t1=g1(x1,x2),t2=g2(x1,x2),由重积分的变量替换公式有
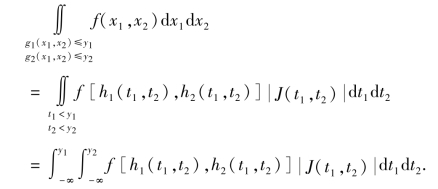
由密度函数的定义,有
![]()
例3.20 设f(x1,x2)是随机向量(X1,X2)的联合概率密度,令
![]()
试用f 表示Y1 和Y2 的联合概率密度.
解 令y1=x1+x2,y2=x1-x2,则反函数为
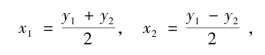
雅可比行列式为
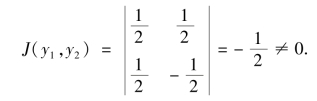
由定理3.7 知,Y1 和Y2 的联合概率密度为
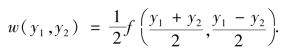
下面我们来讨论几个特殊函数的分布.
(1)和的分布
设X 和Y 的联合概率密度为f(x,y),则Z=X+Y 的密度为
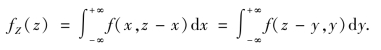
证 为求和函数Z 的概率密度,先考虑Z 的分布函数FZ(z),
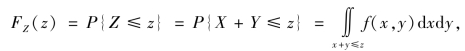
这里积分区域为直线x+y=z 的左下半平面(见图3.9).将上述积分化为累次积分,有
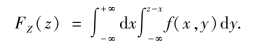
令y=v-x,于是
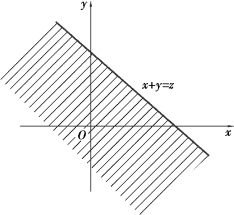
图3.9
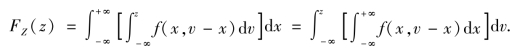
由概率密度的定义,可得Z 的概率密度为
![]()
类似地,也有
![]()
特别地,当X 与Y 相互独立时,则有
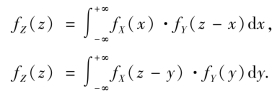
上两式称为卷积(convolution)公式.
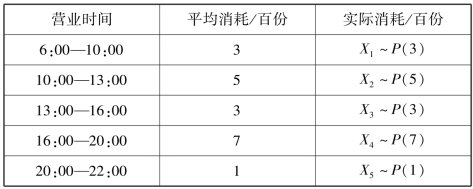
例3.21 “库存准备”问题 假设该餐厅每天营业时间为6:00—22:00,分5 个时段,经统计每个时段平均销售量见表3.22,设X1,X2,X3,X4,X5 分别是相应时间段内薯条的实际消耗量,相互独立,且均服从泊松分布的随机变量.问最少需要多少库存能够有90%的把握保证供应?
表3.22
解 因为X1,X2,X3,X4,X5 相互独立,所以由泊松分布的可加性知
![]()
由题意,需求最小的x,使得P{X≤x} >0.9.
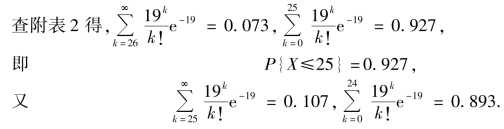
因此,至少应准备25 份薯条的原料.
例3.22 设随机变量X 与Y 相互独立,且都服从N(0,1)分布,求函数Z=X+Y 的概率密度.
解 由题意得X,Y 的概率密度为
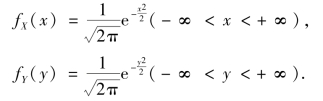
由卷积公式,有
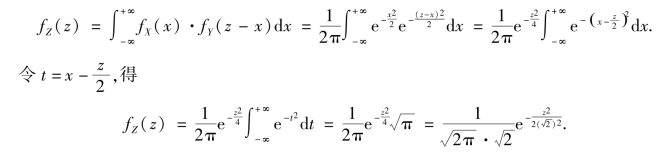
由此可知,Z=X+Y 服从μ=0,σ2=![]() =2 的正态分布,即Z~N(0,2).
=2 的正态分布,即Z~N(0,2).
类似地,利用卷积公式可得到下列定理.
定理3.8 若X,Y 相互独立,且![]() ,则
,则
![]()
此结论可推广到更一般的情形,即有如下定理.
定理3.9 若Xi ~N(μi,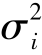 )(i=1,2,…,n),且它们相互独立,则对任意不全为零的常数a1,a2,…,an,有
)(i=1,2,…,n),且它们相互独立,则对任意不全为零的常数a1,a2,…,an,有
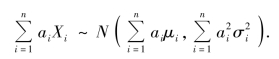
特别地,若X1,X2,…,Xn 相互独立,且Xi ~ N(μ,σ2)(i=1,2,…,n).设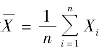 ,则有
,则有
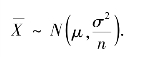
(2)商的分布
设(X,Y)为二维连续型随机向量,其联合概率密度为f(x,y),则Z=![]() 的概率密度为
的概率密度为
![]()
证 令u=y,z=![]() ,即x=uz,y=u.这一变换的雅可比行列式为
,即x=uz,y=u.这一变换的雅可比行列式为
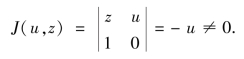
利用定理3.7 得联合概率密度(https://www.daowen.com)
![]()
因此,随机变量Z 的边缘概率密度为
![]()
特别地,当X 与Y 相互独立时, fZ(z)式即可改写成为
![]()
例3.23 设X,Y 相互独立,且X~N(0,1),Y~N(0,1),求Z=![]() 的概率分布.
的概率分布.
解 由X,Y 相互独立可知(X,Y)的联合概率密度为
![]()
可以得到
![]()
这是柯西(Cauchy)分布的概率密度函数.
(3)积的分布
设(X1,X2)为二维连续型随机向量,其联合概率密度为f(x1,x2),则Y=X1X2 的概率密度为
![]()
证 令y=x1x2,z=x1,这一变换的雅可比行列式为
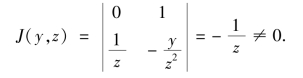
由定理3.7 得联合密度函数为
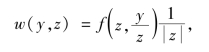
因此
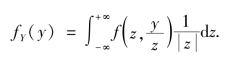
(4)平方和分布
例3.24 设X 与Y 相互独立,且都服从标准正态分布,求Z=X2+Y2 的概率密度.
解 (X,Y)的联合概率密度为
![]()
①当z≤0 时,FZ(z)=0,则fZ(z)=0.
②当z>0 时,有
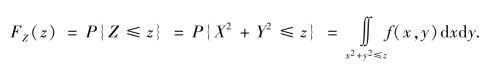
利用极坐标计算上述二重积分,得
![]()
因此,上式对z 求导可得
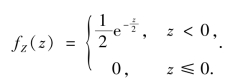
这正是自由度为2 的X2 分布的概率密度.
(5)M=max{X,Y}及N=min{X,Y}的分布
设随机变量X,Y 相互独立,其分布函数分别为FX(x),FY(y).令
![]()
显然,M 及N 为随机变量.
对于M=max{X,Y},若M≤z,必有X≤z,Y≤z.又X 与Y 相互独立,故M 的分布函数
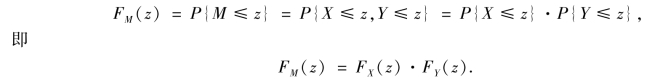
同理,N=min{X,Y}的分布函数为
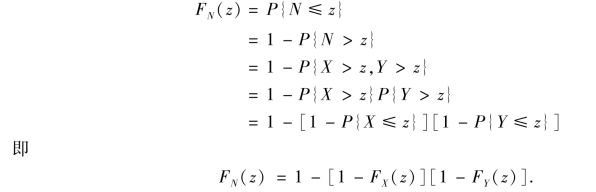
从上述结果,可不难推广到n 个相互独立的随机变量的情形如下.
设X1,X2,…,Xn 是n 个相互独立的随机变量,其分布函数分别为FX1(x1),FX2(x2),…,FXn(xn),则M=max{X1,X2,…,Xn},N=min{X1,X2,…,Xn}的分布函数分别为
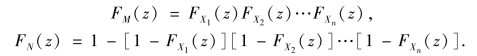
特别地,当随机变量X1,X2,…,Xn 相互独立,且具有相同的分布时,则有
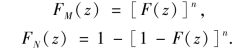
例3.25 某系统Q 由两个子系统q1 与q2 组成,连接的方式有3 种:
①q1 与q2 串联.
②q1 与q2 并联.
③q1 与q2 一个工作、一个备用.
已知子系统q1,q2 的寿命X,Y 均服从指数分布,其概率密度分别为
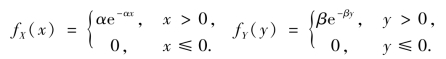
其中α>0,β>0,α≠β.设系统Q 的使用寿命为Z,在上述3 种连接情况下,求寿命Z 的概率密度.
解 ①串联:
若子系统q1 与q2 有一个损坏,系统Q 便停止工作,故Q 的寿命Z=min{X,Y}.
由题设对X,Y 的概率密度积分得X,Y 的分布函数分别为
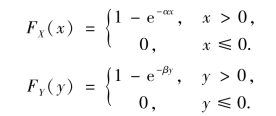
因X 与Y 相互独立,Z 的分布函数
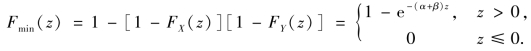
从而,对z 求导得Z 的概率密度为
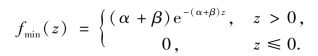
②并联:
因为只有当q1 与q2 两个子系统都损坏时,系统Q 才停止工作,故Q 的寿命
![]()
得Z 的分布函数为
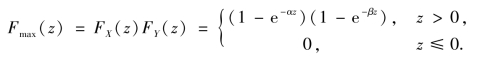
于是z 的概率密度为
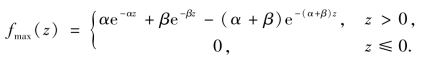
③一个工作、一个备用:
因为当q1 损坏时,q2 才开始工作,所以整个系统Q 的使用寿命Z=X+Y.
当z≤0 时,fZ(z)=0.
当z>0 时,由卷积公式,有
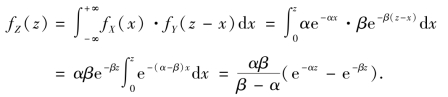
从而,Z=X+Y 的概率密度为
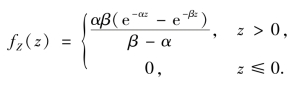
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







