定义3.10　设二维随机向量（X，Y）的联合分布函数和边缘分布函数分别为F（x，y），FX（x），FY（y），若对于任意的实数x，y 有

或

则称随机变量X 与Y 相互独立（mutual independence）.

定理3.1①　设二维离散型随机向量（X，Y）的分布律为

边缘分布律为pi·和p·j，则X 与Y 相互独立的充要条件是：对任意的i，j=1，2，…，有

即

②设二维连续型随机向量（X，Y）的概率密度及边缘概率密度分别为f（x，y），fX（x），fY（y），则X 与Y 相互独立的充要条件是：对任意的实数x，y，有等式

几乎处处成立.

证　我们就连续型的情形进行证明.

必要性

设X 与Y 相互独立，则对任意的实数x，y，有

即

其中fX（x）≥0， fY（y）≥0，从而fX（x）·fY（y）≥0.由定义可知

充分性

设f（x，y）=fX（x）·fY（y）对任意的实数x，y 均成立，则有

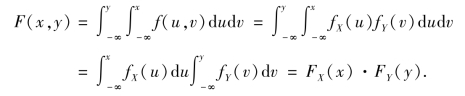
由定义3.10 可知，X 与Y 相互独立.

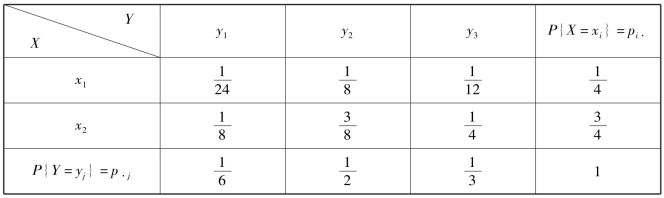
例3.14　设随机变量X 和Y 相互独立，表3.11 列出了二维离散型随机向量（X，Y）的联合分布律及关于X 和关于Y 的边缘分布律的部分数值，试将其余数值填入表3.11 空白处.

表3.11

解　由于

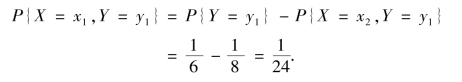
考虑到X 与Y 相互独立，有

所以　P{X=xi}=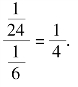

同理，可以得到其他数值.因此（X，Y）的联合分布律和边缘分布律见表3.12.

表3.12

例3.15　已知随机变量X 和Y 的概率分布见表3.13 和表3.14.

表3.13

表3.14

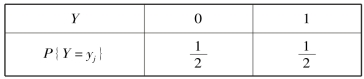
且P{XY=0}=1.求

①求X 与Y 的联合分布.

②X 与Y 是否独立？

解　方法一

①由P{XY=0}=1，可见

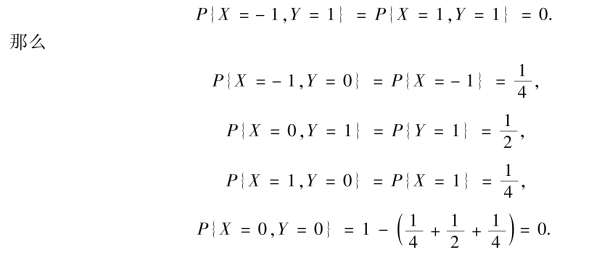
于是，得X 与Y 的联合分布及边缘分布如表3.15 所示.

表3.15

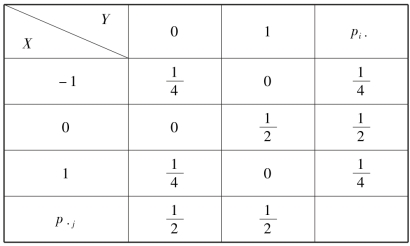
②由以上结果可知

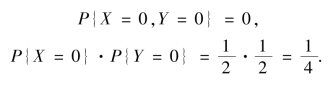
即有

于是，X 与Y 不独立.

方法二

①由P{XY=0}=1，可见(www.daowen.com)

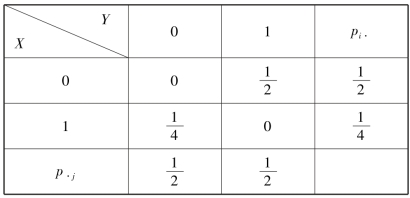
因此，X 与Y 的联合分布如表3.16 所示.

表3.16

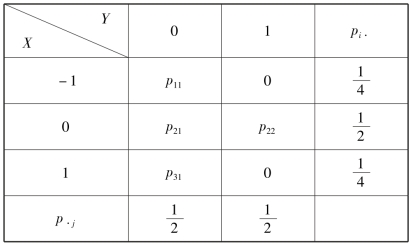
由表3.16，容易求得X 与Y 的联合分布，见表3.17.

表3.17

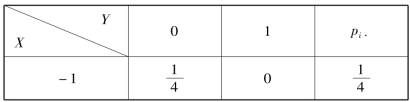
续表

②同方法一.

例3.16　一电子仪器由两个部件构成，用X 和Y 分别表示两个部件的寿命（单位：1 000 h）.已知X 和Y 的联合分布函数为

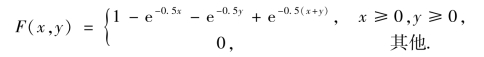
①问X 与Y 是否独立？

②求两个部件的寿命都超过100 h 的概率β.

解　方法一

①X 与Y 的边缘分布函数分别为

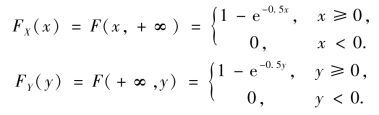
由此可知

于是，X 与Y 相互独立.

②β=P{X>0.1,Y>0.1}=P{X>0.1}·P{Y>0.1}

　　=[1-FX(0.1)]·[1-FY(0.1)]=e -0.05·e -0.05=e -0.1.

方法二

①用f（x，y）， fX（x）， fY（y）分别表示（X，Y）的联合概率密度和两个边缘概率密度，则有

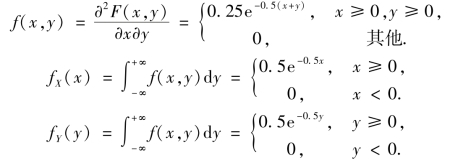
于是有，f（x，y）=fX（x）·fY（y）.

所以，X 与Y 相互独立.

②β=P{X >0.1,Y >0.1}=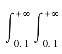0.25e-0.5(x+y)dxdy=e-0.1.

例3.17　设随机向量（X，Y）服从区域D 上的均匀分布，且

①D={(x,y)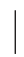a≤x≤b,c≤y≤d}.

②D={(x,y)x2+y2≤R2}.

讨论X 与Y 的独立性.

解　①由题设条件，得知

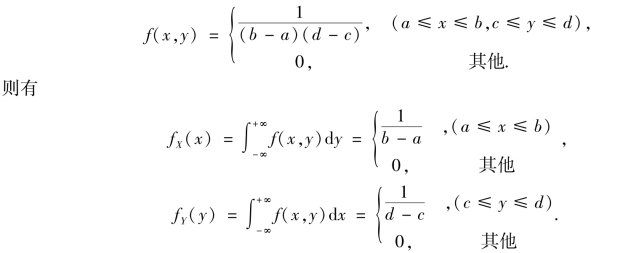
易知，对任意的实数x，y，有f（x，y）=fX（x）·fY（y）.所以，X 与Y 相互独立.

②由题设条件，得知

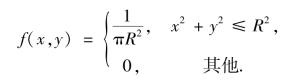
利用本章例3.9 的结果，有

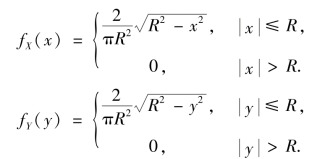
显然，当x2+y2≤R2 时，f（x，y）≠fX（x）·fY（y），所以，X 与Y 不独立.

定理3.2　设二维随机向量（X，Y）服从二维正态分布，即

则X 与Y 相互独立的充要条件是ρ=0.

证　二维正态分布的联合概率密度为

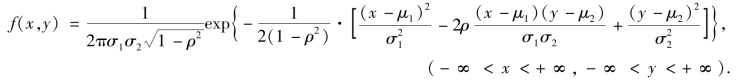
由本章例3.10 的结果可知，X，Y 的边缘概率密度分别为

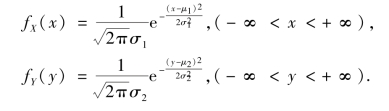
必要性 若X 与Y 相互独立，对于任意的实数x，y，必有

由于

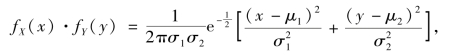
从而

充分性 显然，在f（x，y）中ρ=0 时，对任意的实数x，y 必有

即X 与Y 相互独立.

还可以证明，如果X 与Y 相互独立，那么它们的连续函数g（X）与h（Y）也一定相互独立.特别地，两个相互独立的随机变量的线性函数aX+b 与cY+d（ac≠0）也相互独立.这一结论今后将经常用到，但证明已超出本书范围，故从略.