二维码3.1　学神学霸问题

由于连续型随机变量在任意一点处的概率为零，即P{X=x0}=0，P{Y=y0}=0.所以，不能直接利用事件的条件概率公式引入随机向量的条件概率密度，需要利用极限的方法来处理.为此，先建立条件分布函数，再求条件概率密度.

设（X，Y）为二维连续型随机向量，对于任意Δy→0，若P{y <Y≤y+Δy} >0，则对任意的实数x 有

定义3.9　设（X，Y）为二维连续型随机向量，y 为定值，对于任给的Δy >0，概率值P{y <Y≤y+Δy} >0，若极限

存在，则称此极限值为在条件{Y=y}下X 的条件分布函数，记为

如果二维连续型随机向量（X，Y）的联合分布函数为F（x，y），联合概率密度为f（x，y），且f（x，y）在点（x，y）处连续，而Y 的边缘概率密度fY（y） >0 且连续，则

即在条件{Y=y}下，X 的条件分布函数

类似地，在条件{X=x}下，Y 的条件分布函数

若令

那么X 的条件分布函数式和Y 的条件分布函数式可改为(www.daowen.com)

称f（x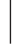y ）为在条件{Y=y}下，X 的条件概率密度.f（y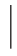x）为在条件{X=x}下，Y 的条件概率密度.

例3.12　求第3章例3.9 中关于X，Y 的条件概率密度.

解　由题意得（X，Y）的联合概率密度为

由此例可看出，在{Y=y}条件下，X 在区间上服从均匀分布.在{X=x}条件下，Y 在区间上也服从均匀分布.

例3.13　设数X 在区间（0，1）内均匀随机地取值，当观察到X=x（0 <x<1）时，数Y 在区间（x，1）内均匀随机地取值，求Y 的概率密度fY（y）.

解　由题设，X 的概率密度为

对于任意给定的x（0 <x<1），当X=x 时，Y 的条件概率密度为

由条件概率密度式，可得（X，Y）的联合概率密度为

于是，有