定义3.7 设(X,Y)是二维随机向量,如果存在某个非负可积函数f(u,v),使得对任意的实数x,y 都有
![]()
则称(X,Y)为二维连续型随机向量.函数f(x,y)称为(X,Y)的概率密度(或概率密度函数),或称为X 与Y 的联合概率密度或联合概率密度函数,记为(X,Y) ~f(x,y).
由定义看出,(X,Y)的概率密度函数f(x,y)满足以下两个性质
①f(x,y) ≥0.
②![]()
反之,任一满足上述两个性质的二元函数f(x,y),必是某个二维随机向量的概率密度函数.
由定义3.7 容易得到,(X,Y)的联合分布函数F(x,y)与它的概率密度f(x,y)之间还应满足如下的关系.
设D 是xoy 平面上一个可度量的平面区域,则有
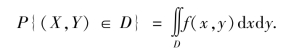
由(X,Y)的联合分布函数公式可知,若密度函数f(x,y)在点(x,y)处连续时,有
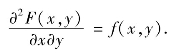
例3.4 设二维随机向量(X,Y) ~f(x,y),并且
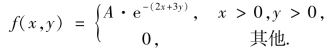
求
①A 的值.
②(X,Y)的分布函数.
③(X,Y)落在区域D={(x,y)![]() ,y≥0,2x+3y≤6}上的概率.
,y≥0,2x+3y≤6}上的概率.
④P{X≥Y}.
解 ①由(X,Y)的概率密度函数f(x,y)满足的两个性质,有
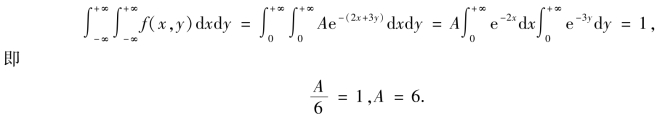
②当x>0,y>0 时,分布函数
![]()
当x≤0 或Y≤0 时,则
![]()
所以
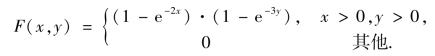
③区域D 如图3.3 所示,则
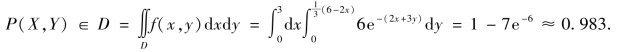
 (https://www.daowen.com)
(https://www.daowen.com)
图3.3
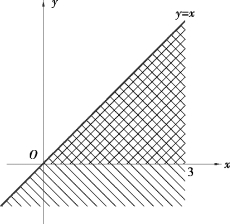
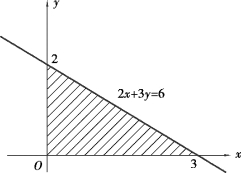
图3.4
④X≥Y 如图3.4 所示,则
![]()
例3.5 一机器制造直径为X 的轴,另一机器制造内径为Y 的轴衬,设(X,Y)的概率密度为
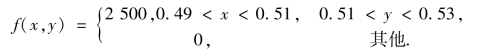
若轴衬的内径与轴的直径之差大于0.004,且小于0.036 时,则两者可以相适衬,求任一圆轴与任一轴衬相适衬的概率.
解 任一圆轴与任一轴衬相适衬的条件是
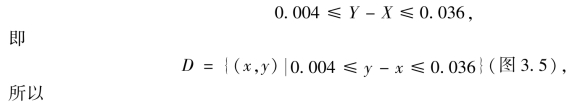
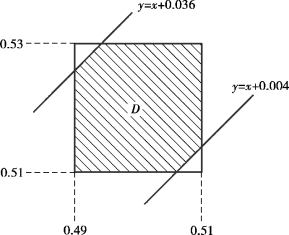
图3.5
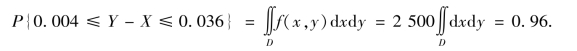
注 如果G 是平面上的一个有界区域,其面积为SG,且SG≠0.若二维连续型随机向量(X,Y)的联合密度函数为
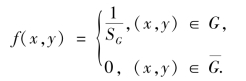
则称(X,Y)服从区域G 上的二维均匀分布.
容易验证二维均匀分布的联合密度函数f(x,y)满足
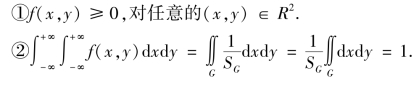
例3.6 在区间(0,1)中随机地取两个数,求这两数之差的绝对值小于![]() 的概率.
的概率.
解 设X,Y 表示随机取到的两个数,由题意知(X,Y)服从区域G 上的二维均匀分布,其中G={(x,y)![]() <x<1,0 <y<1}.
<x<1,0 <y<1}.
则所求概率为![]() ,如图3.6 所示.
,如图3.6 所示.
若二维连续型随变量(X,Y)的联合密度函数为
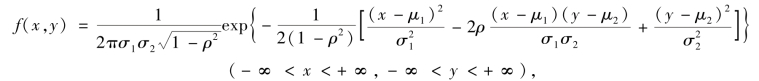
其中μ1,μ2,σ1,σ2,ρ 均为常数,且σ1 >0,σ2 >0,-1 <ρ <1,则称(X,Y)服从参数μ1,μ2,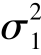 ,
,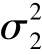 ,ρ 的二维正态分布,记为(X,Y) ~N(μ1,μ2,
,ρ 的二维正态分布,记为(X,Y) ~N(μ1,μ2,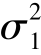 ,
,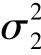 ,ρ),(X,Y)称为二维正态随机向量.
,ρ),(X,Y)称为二维正态随机向量.
可以证明,二维正态随机向量的联合概率密度f(x,y)满足二维连续型随机向量联合概率密度的两个性质.二维正态分布的联合密度函数的图形如图3.7 所示.
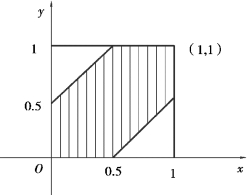
图3.6
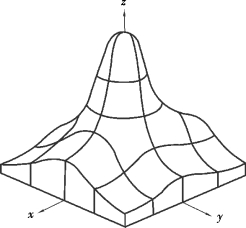
图3.7
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






