与一维随机变量一样，多维随机变量也有离散和连续之分，这里先研究二维离散型随机变量.多维离散型随机变量的研究可以类似进行.

定义3.5　如果二维随机向量（X，Y）的所有可能取值为有限个，或可列无穷多个（数对）时，则称随机向量（X，Y）为二维离散型随机变量.显然，如果（X，Y）为二维离散型随机变量时，则它的每一个分量X 与Y 分别都是一维离散型随机变量；反之亦然.

定义3.6　设二维离散型随机变量（X，Y）的所有可能取值的集合为G={（xi，yj），i，j=1，2，…}，并记（X，Y）取各个可能值的概率为

则称上式为二维离散型随机变量（X，Y）的（联合）分布律，或称为（X，Y）的（联合）概率分布.

显而易见，式中的pij满足下面两个性质

①pij ≥0(i.j=1,2,…).

②

反之，满足上述两个性质的数集{pij，i，j=1，2，…}必为某二维离散型随机向量的分布律.

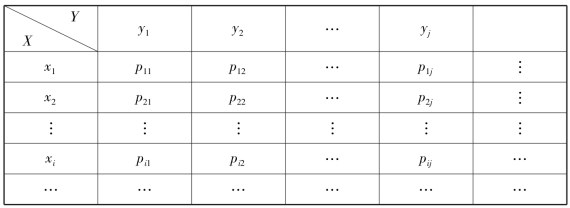
为直观起见，二维离散型随机向量（X，Y）的分布律也可用概率分布表（表3.1）表示.

表3.1

对于集合G={（xi，yi），i，j=1，2，…}的任意一个可度量的子集A，则事件{（X，Y）∈A}的概率为

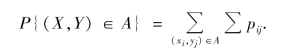
对于任意的实数x，y，（X，Y）的联合分布函数为

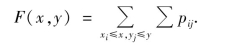
例3.2　箱中共8 件产品，其中一级品3 件，二级品5 件，今从箱中随机连取两次，每次取出1 件，若定义随机变量（X，Y）为

分别按有放回和不放回抽样，求

①（X，Y）的分布律.

②取出的两件产品中最多一件二级品的概率.

解　（X，Y）的可能取值为（0，0），（0，1），（1，0），（1，1）.有放回情形

由于事件{X=i}与{Y=j}相互独立，因此有(www.daowen.com)

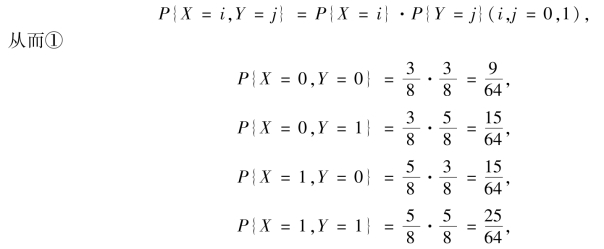
因此（X，Y）的概率分布如表3.2 所示.

表3.2

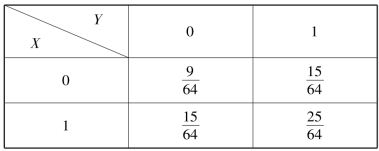
②设A=“取出的两件中最多一件是二级品”，则

由①的结果可知

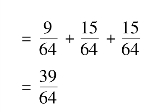
无放回情形

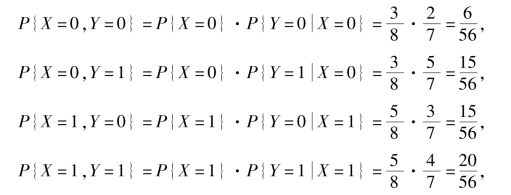
因此（X，Y）的概率分布如表3.3 所示.

表3.3

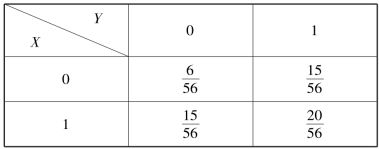
有放回情形

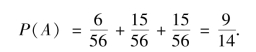
例3.3　设随机变量X 在1，2，3，4 四个整数中等可能地取一个值，另一个随机变量Y 在1 ~X中等可能地取一整数值，试求（X，Y）的概率分布.

解　（X=i，Y=j）的取值情况是：i=1，2，3，4，j 取不大于i 的正整数，且

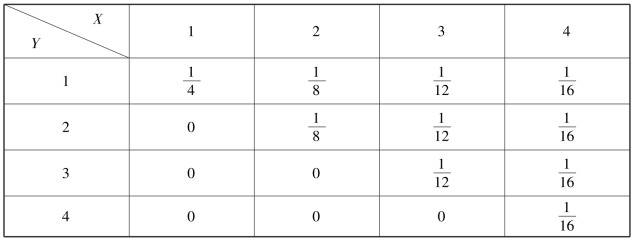
P（X=i，Y=j）=，（i=1，2，3，4，j≤i），于是，（X，Y）的概率分布如表3.4 所示.

表3.4