本节介绍3 种常见的连续型随机变量.

（1）均匀分布

定义2.6　若连续型随机变量X 的概率密度（图2.6）为

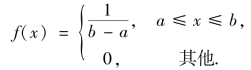
则称X 在[a，b]上服从均匀分布（uniform distribution），记作X~U[a，b].

容易验证均匀分布的概率密度函数f（x）满足：

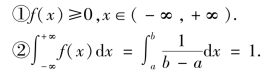
均匀分布函数如图2.7 所示，即

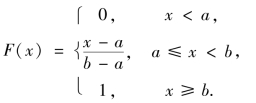
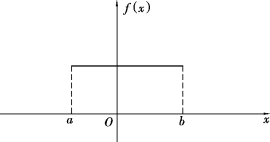
图2.6

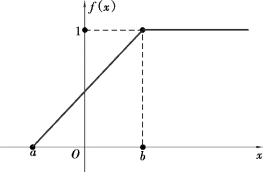
图2.7

若X~U[a，b]，则对于任一长度l 的子区间[c，c+l]⊂[a，b]，有

即在区间[a，b]上服从均匀分布的随机变量X，其取值落在[a，b]中任意等长度的子区间的概率是相同的，且与子区间的长度成正比，与子区间位置无关，这就是“均匀”的含义.

例2.15　某人叫了一辆出租汽车从学

校去火车站乘火车.火车发车时间为11：30，出租汽车开出的时间10：50，出租汽车从学校行驶到火车站的时间X~U[30，60]，从下汽车到上火车需5 min，问该人能赶上这趟火车的概率为多少？

解　若要赶上火车，出租汽车行驶的时间必须少于或等于35 min，所以

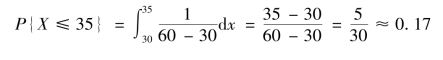
即此人能赶上火车的概率只有17%.

（2）指数分布

定义2.7　若随机变量X 的概率密度（图2.8）为

其中λ>0，则称X 服从参数为λ 的指数分布（exponential distribution）.

容易验证指数分布的概率密度函数f（x）满足

指数分布的分布函数如图2.9 所示，即

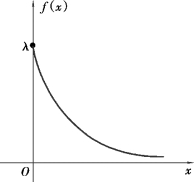
图2.8

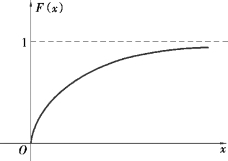
图2.9

指数分布有很广泛的应用，我们常用它来作为各种“寿命”分布的近似.例如，无线电元件的寿命、动物的寿命、保险丝的寿命、电话问题中的通话时间、随机服务系统中的服务时间以及某一复杂系统中两次故障的时间间隔等都近似地服从指数分布.

例2.16　已知某种电子元件的寿命X（年）服从参数为的指数分布，求

①求其寿命小于2 年的概率.

②若某元件已正常工作了2 年，求其还能正常继续工作不超过2 年的概率.

解　由题意可知，X~E即

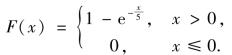
①P{X<2}=F(2)=1-e -0.2×2=1-0.670 3=0.329 7,

即该种子电子元件在2 年内损坏的概率为32.97%.

②依题意，所求事件为，则根据条件概率的定义有

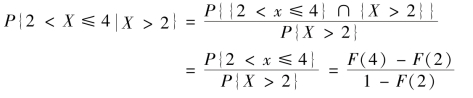
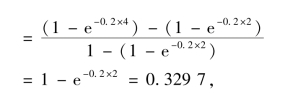
即工作了2 年的元件，再继续工作2 年内损坏的概率与最初的2 年是一样的，都是32.97%.

指数分布也具有“无记忆性”，设随机变量X 服从参数为λ 的指数分布，则对于任意的s>0，t>0，有

假如把X 解释为寿命，则上式表明，如果已知寿命长于s 年，则再活t 年的概率与年龄s 无关，所以有时又称指数分布是“永远年轻”.

（3）正态分布

定义2.8　若随机变量X 的概率密度为

其中μ，σ 均为常数，且σ>0，则称X 服从参数为μ，σ2 的正态分布（normal distribution），记作

正态分布的分布函数为

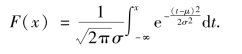
正态分布的概率密度f（x）的图形如图2.10 所示，它具有以下特征：

①正态分布的概率密度函数f（x）以x 轴为渐近线.

②正态分布的概率密度函数f（x）在x=μ 处达到极大，极大值为，并且f（x）关于x=μ 对称，即f（x+μ）=f（x-μ）.(www.daowen.com)

③服从正态分布的随机变量落在等长度区间内的概率越靠近μ 就越大，离μ 越远，X 落在这个区间上的概率越小.

图2.10

④如果固定σ，改变μ 的值，则图形沿着x 轴平移，不改变其形状（图2.10）.如果固定μ，改变σ，由于最大值f（μ）=，可知σ 越小时图形变得越尖（图2.11），因而落在μ 附近的概率越大.

特别，当μ=0，σ=1 时称X 服从标准正态分布，即X~N（0，1），其概率密度和分布函数分别用φ（x），Φ（x）表示，即

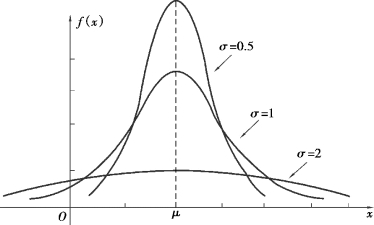
图2.11

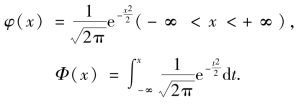
易知

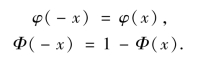
如图2.12 所示，显然Φ（0）=0.5.

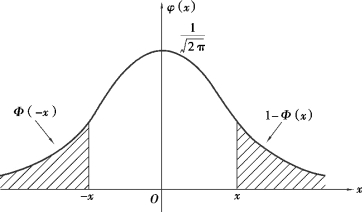
图2.12

书末附表3 是Φ（x）的数值表.若X~N（0，1），直接查表可得Φ（x）的值，从而可求出落在任意区间上的概率，如

一般地，若X~N（μ，σ2），可通过一个线性变换将它化成标准正态分布.

定理2.2　若X~N（μ，σ2），则Z=

证　Z=的分布函数为

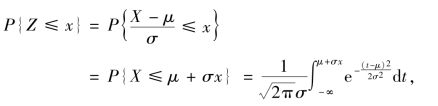
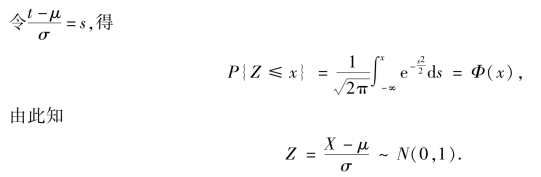
推论　若X~N（μ，σ2），则它的分布函数F（x）可表示为

对于任意区间（a，b]，有

查附表3，得x=1.96.

一般地，对随机变量X~N（μ，σ2），不难算得

如图2.13 所示，注意第三个数据，我们看到，对于正态随机变量来说，它的值落在区间（μ-3σ，μ+3σ）内几乎是肯定的事件，这就是所谓“3σ 原则”.

例2.18　公共汽车车门的高度是按照成年男子与车门顶碰头的机会在1%以下来设计的.设男子身高服从μ=170 cm，σ=6 cm 的正态分布，即X ~N（170，62），问车门高度应如何确定？

解　设车门高度为h cm，按设计要求P（X≥h）≤0.01 或P（X <h）≥0.99.因为X ~N（170，62），故

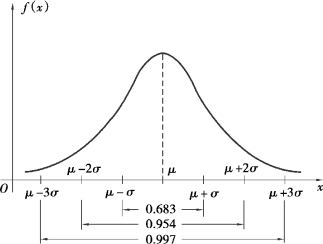
图2.13

查附表3 得

故取=2.33，即h≈184.设计车门高度为184 cm 时，可使成年男子与车门碰头的机会不超过1%.

例2.19　某单位招聘2 500 人，按考试成绩从高分到低分依次录用，共有10 000 人报名，假设报名者的成绩X~N（μ，σ2），已知90 分以上有359 人，60 分以下有1 151 人，问被录用者中最低分为多少？

分析　已知成绩X~N（μ，σ2），但不知道μ，σ 的值，所以本题的关键是求μ，σ，再进一步根据正态分布标准化方法进行求解.

反查标准正态分布表，得

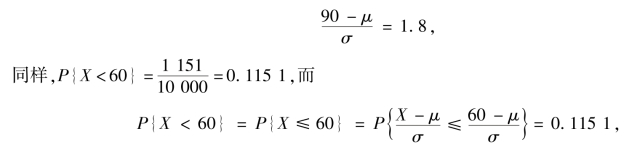
反查标准正态分布表，得

解得

所以X~N（72，10）.

已知录用率=0.25，设被录用者最低分为x0，则

二维码2.3　血液指标分析

反查标准正态分布表，得

二维码2.4　路程问题

解得x0≈78.75，即被录用者中最低分为79 分.

在自然现象和社会现象中，大量随机变量都服从或近似服从正态分布.例如，人体的身高、体重，测量的误差，农作物的收获量，海洋波浪的高度等均服从正态分布.在概率论和数理统计的理论研究和实际应用中，正态随机变量起着特别重要的作用.在第5章中我们将进一步说明正态随机变量的重要性.