例2.12 一个半径为2 米的圆盘靶,设击中靶上任一同心圆盘上的点的概率与该圆盘的面积成正比,并设射击都能中靶,以X 表示弹着点与圆心的距离,试求随机变量X 的分布函数.
解 ①若x<0,因为事件{X≤x}是不可能事件,所以
![]()
②若0≤x≤2,由题意P{0≤X≤x}=kx2,k 是常数,为了确定k 的值,取x=2,有P{0≤X≤2}=22k,但事件{0≤X≤2}是必然事件,故P{0≤X≤2}=1,即22k=1,所以k=![]() ,即
,即
![]()
于是 F(x)=P{X≤x}=P{X<0}+P{0≤X≤x}=![]() .
.
③若x≥2,由于{x≤2}是必然事件,于是
![]()
综上所述
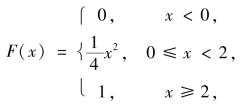
它的图形是一条连续曲线如图2.3 所示.
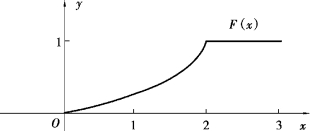
图2.3
另外,容易看到本例中X 的分布函数F(x)还可写成如下形式
![]()
其中

这就是说F(x)恰好是非负函数f(t)在区间(-∞,x)上的积分,这种随机变量X 我们称为连续型随机变量.一般地有如下定义.
定义2.5 对于随机变量X,如果存在某一非负函数f(x),使得对于任意实数x,有

则称X 为连续型随机变量(continuous random variable).其中函数f(x)称为X 的概率密度函数,简称概率密度(density function)或分布密度.
由上式知连续型随机变量的分布函数是连续函数.
由定义知,概率密度f(x)具有以下性质:
性质1 f(x)≥0(-∞<x<+∞).
性质2 ![]()
性质3 对任何实数a,b (a≤b),有
![]()
性质4 若f(x)在点x 处连续,则有
![]()
由性质2 知,介于曲线y=f(x)与x 轴之间的面积等于1(图2.4).由性质3 知道,X 落在区间(a,b]的概率P{a<X≤b}等于区间(a,b]上曲线y=f(x)之下的曲线边梯形的面积(图2.5).
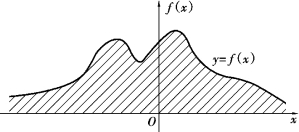
图2.4

图2.5
由性质4 知,在f(x)的连续点x 处有(https://www.daowen.com)
![]()
在上式中,若不计高阶无穷小,有
![]()
即表示X 落在小区间(x,x+Δx]上的概率近似地等于f(x)Δx.
由连续性随机变量的定义知,对于任一常数a,有
![]()
这是连续型随机变量的一个特殊性质.
事实上,设X 的分布函数为F(x),Δx>0,则由{X=a}⊂{a-Δx<X≤a}得
![]()
由于F(x)是一连续函数,于是有
![]()
所以,有
![]()
因此,在计算连续型随机变量落在某一区间的概率时,可以不必区分该区间是开区间或闭区间或半开半闭区间,即有
![]()
特别要指出的是,尽管{X=a}的概率为零,但它不一定是不可能事件.这事实也说明,不可能事件的概率一定为零;反之,概率为零的事件不一定是不可能事件.由此可知,概率为1 的事件也不一定是必然事件.
例2.13 设连续型随机变量X 的分布函数为
![]()
求:①A,B 的值.
②X 的概率密度f(x).
解 ①由分布函数性质F(-∞)=0 及F(+∞)=1,可得

解得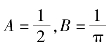 ,所以
,所以

②根据性质4,有
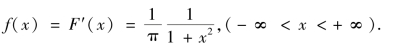
例2.14 设随机变量X 的概率密度为
![]()
求:①a 的值;
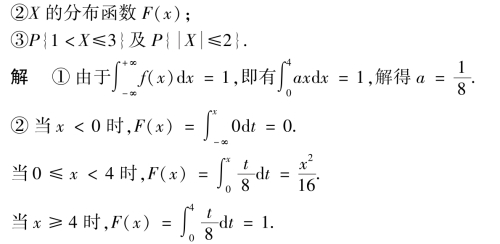
因此,分布函数为
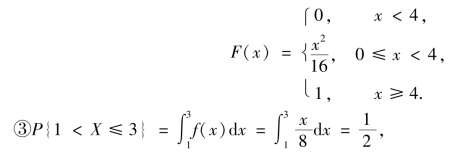
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





