（1）0—1 分布

若随机变量X 只取0 与1，其概率分布为

则称X 服从参数为p 的0—1 分布.0—1 分布的分布律也可用表格的形式表示，见表2.4.

表2.4

例2.5　100 件产品中有95 件正品，5 件次品，从中随机取一件，求抽样结果的概率分布.

解　令

则有

即X 服从参数为0.95 的0—1 分布.

（2）二项分布

定义2.3　若随机变量X 的分布律为

则称X 服从参数为n，p 的二项分布（binomial distribution），记为X~B（n，p）.

易知，二项分布满足随机变量X 的分布律的两个性质式.P{X=k}≥0（k=0，1，2，…，n）是显然的，由二项展开式可知

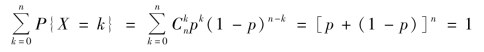
而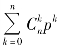（1- p）n-k 恰好是二项式[p+（1- p）]n 的展开式中出现pk 的一项.

特别，当n=1 时，二项分布即为

因此，此时0—1 分布就是二项分布在n=1 的特殊情况.

例2.6　设某射手每次射击的命中率为0.6，现在连续射击6 次，求击中目标次数的概率分布.又设至少命中2 次才可以参加下一步的考核，求此射击手能参加考核的概率.

解　设X 表示击中目标的次数，那么X~B（6，0.6），所以

又因为“此射手能参加考核”等价于事件{X≥2}，所以此射手能参加考核的概率为

例2.7（工作效率问题）　某公司研发楼有4 层，每层有电脑20 台，发生故障的概率都是0.01.考虑两种方案配备电脑维护人员：其一是由4 人维护，每人1 层（20 台）；其二是由3 人共同维护80 台.试比较这两种方法在电脑发生故障时不能及时维修的概率大小？

解　第一种方案：每人维护20 台电脑.设事件B 表示电脑出故障，X 表示20 台电脑中同时发生故障的台数，则

由题意可知，需求P{X≥2}.

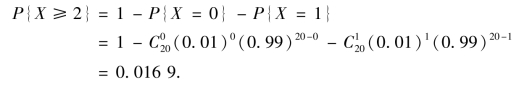
设事件A 表示电脑不能及时维修，Ai 表示第i 层的电脑不能及时维修（i=1，2，3，4），则

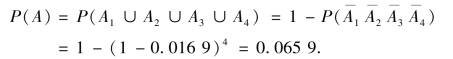
即采用第一种方案电脑不能及时维修的概率为0.065 9.

第二种方案：3 人共同维护80 台电脑.设事件Y 表示80 台电脑中同时发生故障的台数.则Y~B（80，0.01）.从题意可知，需求P{Y≥4}.

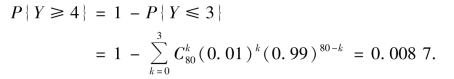
即采用第二种方法电脑不能及时维修的概率降为0.008 7.

从计算结果知，在后一种情况尽管任务重了（每人平均维护约27 台），但工作质量不仅没有降低，反而提高了.这个例子表明概率方法可以用来讨论经济管理的某些问题，以便达到优化地使用人力、物力资源的目的.

（3）泊松（Poisson）分布

若随机变量X 的概率分布为(www.daowen.com)

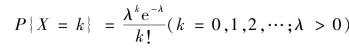
则称X 服从参数为λ 的泊松（Poisson）分布.

显然，P{X=k}≥0（k=0，1，2，…），且

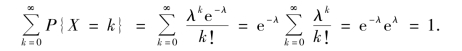
例2.8　一家商场销售某一型号的电视机.由该商场过去的销售记录知道，此型号电视机每月的销售数可以用参数为λ=10 的泊松分布来描述.为了以95%以上的把握保证不脱销，问商场在月底至少应进该型号电视机多少台？

解　设X 表示商场每月销售该型号电视机的台数，且月底的进货为t 台，则当X≤t 时就不会脱销，因而按题意要求为P（X≤t）≥0.95.

又因为X ~ P（10），所以上式也可表示为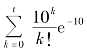≥0.95

由于

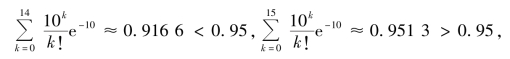
所以满足条件的最小的t 为15.

由此可知，这家商场只要在月底进货15 台该型号电视机（假定上个月无存货，否则应扣除），就可以有95%以上的把握保证这种电视机下个月内不会脱销.

历史上泊松分布是作为二项分布的近似，于1837 年由法国数学家泊松引入的.下面介绍这个有名的定理.

二维码2.1　网球比赛赛制分析

定理2.1（泊松定理）　在n 重伯努利试验中，设pn（0 <pn <1）表示事件A 在每次试验中发生的概率，它与试验总数n 有关，若=λ（λ>0），则有

证明　记λn=npn，则

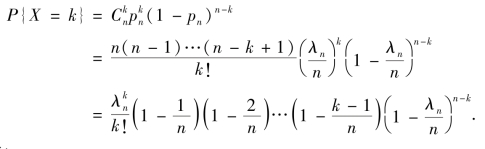
对于固定的k，有

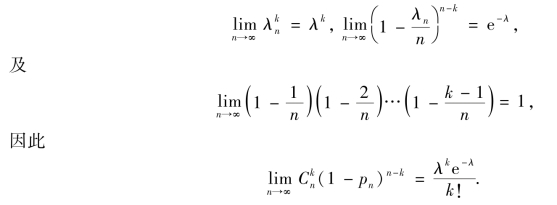
从上面的推导过程可以看出，泊松分布是当npn→λ（n→∞）时二项分布的极限分布.因此在n 很大，而p 较小的情况下，可以利用泊松分布来作为二项分布的近似计算.在实际计算中，一般地当n>20，p<0.05 或者n >100，p <0.1 时，泊松分布与二项分布的计算结果就比较近似.

例2.9（三胞胎问题）　假如生三胞胎的概率为10 -4，求在100 000 次生育中有0，1，2 次生三胞胎的概率？

解　设X 表示100 000 次生育三胞胎的次数，则X~B（105，10 -4），即

题目中n=100 000（很大），p=10 -4（很小），可利用泊松分布近似计算.由泊松定理知，λ=np=10，P{X=k}=

从表2.5 中可以直观地看出二项分布和泊松分布计算结果的近似程度.

表2.5

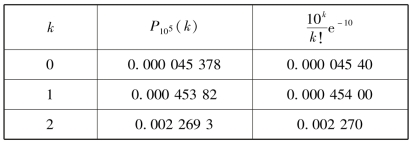
表中泊松分布的值有表可查（见本书附表2）.

例2.10　某厂共有300 台同类型车床，它们独立地工作，且每台发生故障的概率为0.01.在通常情况下，一台车床的故障可由一个工人来处理，问至少要配备多少维修工，才能保证车床发生故障而不能及时维修的概率小于0.01？

解　设X 为“同时发生故障的车床数”，需要配备的工人数为N，由题意可知

所需解决的问题是确定最小的N，使得

由泊松定理知，λ=np=300 ×0.01=3，

二维码2.2　母鸡孵蛋问题

查泊松分布表，得N+1≥9，因此至少要配备8 个维修工才能满足要求.

泊松分布是概率论中最重要的概率分布之一，可以作为描述大量试验中稀有事件出现的次数k=0，1，…的概率分布情况的一个数学模型.在各种服务系统中大量出现泊松分布.例如，大量产品中抽样检查时得到的不合格品数；一个集团中员工生日是元旦的人数；一页中印刷错误出现的数目；观察某电话交换台在单位时间内收到用户的呼唤次数；某公共汽车站在单位时间内来车站乘车的乘客数等均是服从泊松分布的.所以，在运筹学及管理科学中泊松分布有着广泛的应用；在工业生产中，每米布的疵点数、纺织机上的断头数、每件钢铁铸件的缺陷数等也近似地服从泊松分布.由泊松定理，泊松分布也可以作为当n 很大，p 或1-p 很小时二项分布的近似分布，泊松分布是概率论中一种很重要的分布.