定义2.2　设X 是离散型随机变量，它所有可能取的值为xi（i=1，2，3，…），X 取各个可能值的概率为

称上式为随机变量X 的分布律（law of probability distribution）或X 的概率分布，简称分布.

分布律也可用表格的形式来表示，见表2.1.

表2.1

容易验证，分布律满足以下性质

①pi≥0(i=1,2,…).

②=1.

反之，任何一个满足上述两个性质的一组数{pi}一定是某一离散型随机变量的分布律.

例2.3　在汽车经过的路上有4 个交叉路口，设在每个交叉路口碰到红灯的概率都是p，且设各路口信号灯的工作是相互独立的.求汽车首次停下时，已通过的交叉路口个数的分布律.

解　设X=“汽车首次停下时已通过的交叉路口的个数”，则X 所有可能的取值为0，1，2，3，4；事件{X=k}（k=0，1，2，3），表示前k 个路口都是绿灯，而第k+1 个路口是红灯，其概率为（1-p）kp；事件{X=4}表示所有4 个路口都是绿灯，其概率为（1-p）4.于是，X 的分布律如表2.2 所示.

表2.2

(www.daowen.com)

或写成

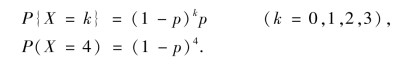
例2.4　一袋中有5 个乒乓球，编号分别为1，2，3，4，5.从中任取3 个，以X 表示取出的3个球中的最大号码.

①求X 的分布律；

②求P（X≤4）的概率.

解　①本题的试验为古典概型，基本事件总数为=10，X 可能取的值为3，4，5，则

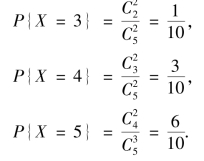
所以，X的分布律见表2.3.

表2.3

②P(X≤4)=

下面我们来介绍几种常见的离散型随机变量及其分布.