在随机现象中，有很大一部分问题与数值发生关系.例如，在产品检验中，我们关心抽样中出现的次品数；在车间供电问题中，我们关心某时刻同时工作的车床数；在电话问题中，关心某段时间电话交换台来到的呼叫次数及测量时的误差等都与数值有关.

有些初看起来与数值无关的随机现象，也常常能联系数值来描述.

例2.1　考察掷硬币的试验，它有两个可能的结果：H（正面）出现或T（反面）出现，与数值没有关系，但我们能用下面方法使它与数值联系起来.当“H 出现” 时用数“1”表示，“T 出现”时用数“0”表示.这就相当于引入一个变量X，对于试验的两个可能的结果，令X 的值分别为1或0.若与试验的样本空间Ω={H，T}联系起来，那么X 是定义在样本空间上的函数，具体地可表示为

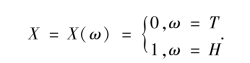
由于试验结果的出现是随机的，因而函数X（ω）的取值也是随机的，称X（ω）为随机变量.若要计算n 次投掷中出现正面的次数就只须计算其中“1”出现的次数即可.

例2.2　考察“测试某种型号电子元件的寿命”的试验，试验的结果电子元件的使用寿命本身就是用数量描述的.引入了变量X 表示“电子元件的寿命”，这个变量的取值由试验的结果所确定，X 随着试验的不同结果而取不同的值，X 是定义在样本空间Ω=上的函数，即

它也是随机变量，X 的值域为[0，+∞）.

从上面的例子可以看出对于随机试验来说，其可能结果都不止一个.我们可以把试验结果与实数X 对应起来，将随机试验的结果数量化，引入随机变量的概念，这样样本点ω 与实数X之间就联系起来，建立了样本空间Ω 与实数子集之间的对应关系X=X（ω），如图2.1，图中Rx表示随机变量X（ω）的值域.(www.daowen.com)

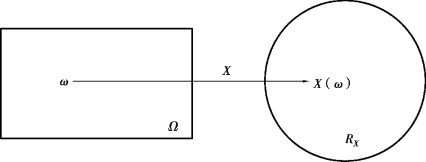
图2.1

下面，给出随机变量的定义.

定义2.1　设E 是随机试验，样本空间为Ω.若对于每一个ω∈Ω，有一个实数X（ω）与之对应，这样就得到一个定义在Ω 上的单值实值函数X=X（ω），称为随机变量（random variable）.

随机变量常用大写英文字母X，Y，Z 表示，用小写字母x，y，z，…等表示随机变量所取的值.

随机变量随着试验的结果而取不同的值，在试验之前只知道它可能取值的范围，不能事先预知它取什么值.此外，随机变量取各个值有一定的概率，这一性质显示了随机变量与普通函数有着本质的区别.普通函数是定义在实数轴上的，而随机变量是定义在样本空间上的，且样本空间的元素不一定是实数.

随机变量按其可能取值的不同特点可分为两类.如果随机变量X 所有可能取值是有限个或可数无穷个，则称X 为离散型随机变量（discrete random variable），如例2.1.如果随机变量X的取值充满某个区间或者整个实数轴，则称X 为连续型随机变量（continuous random variable），如例2.2.随机变量的引入，使我们可以利用数学方法来研究随机现象，下面我们将深入地研究离散型和连续型两种随机变量及其分布函数，还有一种奇异型随机变量超出本书的研究范围，就不再做介绍了.