在实际问题的研究中,如果事件A 发生的可能性不受事件B 发生与否的影响,我们认为在概率意义下事件A 对于事件B 是没有关系的,即事件A 独立于事件B.显然,若A 对于B 独立,则B 对于A 也一定独立,即事件A 与事件B 相互独立.
定义1.7 若事件A 与B 满足P(AB)=P(A)P(B),则称事件A 与B 相互独立.
注 A,B 相互独立与A,B 互不相容不能同时成立.
定理1.4 若事件A 与B 独立,则下列各对事件
也相互独立.
同理可推得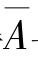 与B、
与B、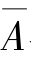 与
与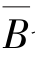 也相互独立.
也相互独立.
定理1.5 若事件A 与B 相互独立,且0 <P(A) <1,则
定理的正确性由乘法公式、相互独立性定义容易推出.
在实际应用中,还经常遇到多个事件之间的相互独立问题,例如:对三个事件的独立性可做如下定义.
定义1.8 若事件A,B,C 满足
则称事件A,B,C 为相互独立事件.
一般当事件A,B,C 两两独立时,等式
不一定成立.
例1.27(伯恩斯坦反例1) 一个均匀的正四面体,其第一面染成红色,第二面染成白色,第三面染成蓝色,而第四面同时染上红、白、蓝3 种颜色.现以A,B,C 分别记一次正四面体出现红、白、蓝颜色朝下的事件.问事件A,B,C 两两独立吗?
解 由于在四面体中红、白、蓝分别出现两面,因此
又由题意知
故有
所以,事件A,B,C 两两独立.
又
所以
事件A,B,C 两两独立但不是相互独立.(https://www.daowen.com)
类似的我们可以定义n 个事件的独立性.
定义1.9 设A1,A2,…,An 为n(n>2)个事件,若对其任何组合1≤i<j<…≤n,成立
则称A1,A2,…,An 相互独立.
由上述定义,不难推出以下事实:
①如果事件A1,A2,…,An 相互独立,则它们的任意一部分事件换成各自的对立事件后,所得的n 个事件仍相互独立.
②若事件A1,A2,…,An 相互独立,则其中任意k(1 <k≤n)个事件也相互独立.
推论1 若A1,A2,…,An 是n 个相互独立的事件,则
在实际应用中,对于事件的独立性,我们往往不是根据定义来判断,而是根据实际意义来加以判断.
例1.28 甲,乙,丙3 部机床独立工作,由一个工人照管,某段时间内它们不需要工人照管的概率分别为0.9,0.8 及0.85.求在这段时间内有机床需要工人照管的概率.
解 用事件A,B,C 分别表示在这段时间内机床甲,乙,丙不需工人照管.依题意A,B,C相互独立,并且
P(A)=0.9,P(B)=0.8,P(C)=0.85,则这段时间内有机床需要工人照管的概率为
例1.29 俗话说:三个臭皮匠赛过诸葛亮.这句话是否有依据?为了解决这个问题,我们让两个队伍进行解题比赛.
诸葛亮:依我的经验,我解出的把握有80%.
臭皮匠老二:老大,你的把握有50%,我只有45%,看来这奖品与咱们无缘了.
臭皮匠老大:二弟别急,咱去把老三叫来,我就不信合咱三人之力,胜不过诸葛亮?
问题:假如臭皮匠老三解出的把握只有40%,那么这三个臭皮匠有一人解出的把握真能胜过诸葛亮吗?
已知诸葛亮解出问题的概率为0.8,臭皮匠老大解出问题的概率为0.5,老二为0.45,老三为0.4,且每个人必须独立解题,问三个臭皮匠能赛一个诸葛亮吗?
解 设事件B={问题被解出},Ai={第j 个臭皮匠解出问题},i=1,2,3,
由题意可知
所以,三个臭皮匠能赛一个诸葛亮.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







