例1.22　白浅要闭关几天，府上有一盆金莲花需要看管，于是在闭关前交由邻居夜华帮忙照看.如果几天内夜华记得浇水，金莲花存活率为0.8；如果几天内夜华忘记浇水，金莲花存活率为0.2，假设白浅对邻居夜华并不了解，即可以认为夜华记得浇水和忘记浇水的概率为0.5，问白浅出关后金莲花存活的概率多大？

解　在问题中设A=“记得浇水”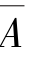，=“忘记浇水”刚好构成Ω 的一个划分.设B=“金莲花存活”，那么B 也被A 和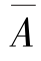划分为两个互不相容的两个部分，即AB 和.由题设可知

因此，金莲花存活的概率为

从形式上看事件B 是比较复杂的，仅仅使用加法定理或乘法定理无法计算其概率.于是先将复杂的事件B 分解为较简单的事件AB 与；再利用加法定理与乘法定理结合起来，计算出需要求的概率.将这个想法一般化，得到全概率定理，又称全概率公式.

定理1.2（全概率公式）　若事件A1，A2，…，An 构成样本空间Ω 一个完备事件组（或划分），并且P（Ai） >0（i=1，2，3，…，n），则对样本空间Ω 中任意一事件B，有

证　由于A1，A2，…，An 两两互不相容，因此，A1B，A2B，…，AnB 也两两互不相容，且B=BΩ=B（A1∪A2∪…∪An）=BA1∪BA2∪…∪BAn.利用加法原理和乘法定理有

例1.23　某地区应届初中毕业生有70%报考普通高中，20%报考中专，10%报考职业高中，录取率分别为90%，75%，85%.试求随机调查一名学生，他如愿以偿的概率.

解　设他如愿以偿的事件为B，报考普通高中为A1，报考中专为A2，报考职业高中为A3，则B 的概率为

例1.24（敏感问题调查）　敏感问题是指涉及个人隐私的问题以及大多数人认为不便于在公开场合表态或陈述的问题，如私人财产、吸毒、作弊等.进行这类问题调查时，如不注意方式、措辞等，就会使拒答率相当高，或者得不到真实的答案，从而导致调查失败.1965 年斯坦利·沃纳（Stanley Warner）提出了一种随机化回答的方法.其设计原则是根据敏感性特征设计两个相互对立的问题，让被调查者按预定的概率从中选择一个回答，调查者无权过问被调查者究竟回答的是哪一个问题，从而起到了为被调查者保密的效果.为调查某次考试的作弊情况，给被访者设定两个问题：

问题一：你在本次考试中作弊了吗？

问题二：你在本次考试中没有作弊吗？

被访者通过随机抽签来回答问题一或者问题二.如果被访者真的作弊了，抽中问题一则答“是”，抽中问题二则答“否”，抽签的结果只有自己知道，他只需回答“是”或“否”，而访问者并不知道回答的是问题一还是问题二，所以被访者可以没有顾虑地真实回答.假设被访者回答问题一的概率为0.7，所有收回的答案中回答“是”的概率是0.31，试估计此次考试的作弊率.

解　记B 为回答问题一，A 为回答“是”，并设作弊概率为p，根据问题描述可以得到，P（A）=0.31，P（B）=0.7，P=p，P=1-p，

利用全概率公式，P（A）=P（AB）+，将数值代入求解，即

得

从本例可以看出，沃纳提出的随机化回答的方法就是利用全概率的思想，打消被访者的顾虑真实回答问题，调查者通过计算就能够得到真实的数据.(www.daowen.com)

例1.22 中，如果白浅出关后，发现金莲花还活着，那么夜华“记得浇水”的概率有多大？此概率就相当于求，由条件概率公式和乘法定理可知

定理1.3（贝叶斯（Bayes）公式）　若事件A1，A2，…，An 构成样本空间Ω 一个完备事件组（或划分），并且P（B） >0，P（Ai） >0（i=1，2，…，n），则对样本空间Ω 中任意一事件B，有

此式称为贝叶斯公式，也称为逆概率公式.证

由条件概率的定义得

对分子用乘法定理，对分母用全概率公式，即得

二维码1.1　用Bayes 公式解释“孩子与狼”的诚信问题

例1.25　由以往的临床记录，某种诊断癌症的试验具有如下效果：被诊断者有癌症，试验反应为阳性的概率为0.95.被诊断者没有癌症，试验反应为阴性的概率为0.95.现对自然人群进行普查，设被试验的人群中患有癌症的概率为0.005，求：已知试验反应为阳性，该被诊断者确有癌症的概率.

解　设A 表示“患有癌症”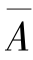， 表示“没有癌症”，B 表示“试验反应为阳性”，则由条件得

这就是说，根据以往的数据分析可以得到，患有癌症的被诊断者，试验反应为阳性的概率为95%，没有患癌症的被诊断者，试验反应为阴性的概率为95%，都称为先验概率.而在得到试验结果反应为阳性，该被诊断者确有癌症重新加以修正的概率0.087 称为后验概率.此项试验也表明，用它作为普查，正确性诊断只有8.7% （即1 000 人具有阳性反应的人中大约只有87 人的确患有癌症），由此可看出，若把搞混淆就会造成误诊的不良后果.

注：在使用全概率公式和贝叶斯公式的题型中，关键的一步是要使用一完备事件组.最常用的完备事件组是A 与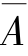 构成的完备事件组，这时

例1.26　在一个初冬大雾天的下午六点左右发生了一起交通事故，肇事车是本市一辆出租车，该车早已逃逸.有一个目击者认定是一辆绿色出租车，若你是交警，你能确信目击者的证言吗？

解　假定经调查该市有红、绿两种颜色的出租车，其中绿色占17%，红色占83%.我们假定通过测试可知，目击者将红色看成红色的概率为0.8，将红色看成绿色的概率为0.2.将绿色看成绿色的概率为0.9，将绿色的看成红色的概率为0.1.用贝叶斯公式可判断目击者证言可信度的大小.设事件A 表示出租车是绿色的，则事件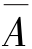表示出租车是红色的.表示出租车是绿色的确实是绿色的事件B 表示肇事出租车确实是绿色的，则

由贝叶斯公式可得

二维码1.2　中国女排夺冠预测

根据计算，在这种情形下目击者尽管说的是真话，但他判断正确的概率也只有0.48，所以交警要想破案，还得收集更有力的证据.