条件概率是概率论中的一个基本工具，用来计算一些复杂的概率.在引入条件概率的概念之前，先看一个例子.

考察有两个孩子的家庭，它共有4 种基本结果{（男，男），（男，女），（女，男），（女，女）}，假定一个孩子为男为女是等可能的，那么上述4 种基本结果也是等可能的，以A 表示有一男一女的家庭，B 表示至少有一个女孩的家庭，则P（A）=

定义1.6　设A，B 为两个事件，且P（A） >0，则称为事件A 已经发生的条件下事件B 发生的概率，记作，即

易验证，符合概率定义1.5 的3 条公理，即

①对于任一事件B，有

②P=1;

③P，其中B1，B2，…，Bn，…为两两互不相容事件.

由此可知，已证明的概率结果都适用于条件概率.例如，对于任意事件B1，B2，有

又如，对于任意事件B，有

例1.17　市场上供应的灯泡中，甲厂的产品占70%，乙厂占30%，甲厂产品的合格率是95%，乙厂的合格率是80%.若用事件A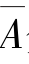， 分别表示甲乙两厂的产品，B 表示产品为合格品.试写出有关事件的概率和条件概率.

解　依题意(www.daowen.com)

例1.18　某电子元件厂有职工180 人，其中男职工100 人，女职工80 人，男女职工中非熟练工人分别为20 人与5 人.现从该厂中任选一名职工，则

①该职工为非熟练工人的概率是多少？

②若已知被选出的是女职工，她是非熟练工人的概率又是多少？

解　①设A 表示“任选一名职工为非熟练工人”的事件，则

②这个问题增加了一个附加条件，即已知被选出的是女职工，记事件B 为“选出女职工”，则②就是要求出“在已知事件B 发生的条件下事件A 发生的概率”，这就要用到条件概率公式，有

此题也可考虑用缩小样本空间的方法来做.既然已知选出的是女职工，那么男职工就可以排除在考虑范围之外.因此“B 已发生条件下的事件A”就相当于在全部女职工中任选一人，并选出了非熟练工人.这时，ΩB 中的样本点总数不是原样本空间Ω 的180 人，而是全体女职工人数80 人.上述事件中包含的样本点数是女职工中的非熟练工人数5 人，因此所求概率为

例1.19　某科动物出生之后活到20 岁的概率为0.7，活到25 岁的概率为0.56，求现年为20 岁的动物活到25 岁的概率.

解　设A 表示“活到20 岁以上”的事件，B 表示“活到25 岁以上”的事件，则有

从定义1.6 可以看出，当P（A） >0 时，P

注：一般的条件概率中的条件A 是随机的，不是必然发生的.但事件A 发生后，它就变成了新的必然事件.条件概率的计算就是在新的必然事件A （新的样本空间）的背景下计算的，这种计算方法称为压缩空间法.