由于概率的统计定义和古典定义的应用范围的局限性，作为概率论的数学定义来建立概率论是不完整的.从概率的统计定义和古典定义可知，一个事件的概率具有下面的基本性质：

①对任何事件A，有0≤P（A）≤1；

②P(Ω)=1;

③若事件A1，A2，…，An 为两两互不相容事件，则有

通过抽象概括概率统计定义和古典定义的共性，给出概率的公理化定义，作为概率的数学理论基础.

定义1.5　在一随机现象中，用来表示任一随机事件A 发生可能性大小的实数称为该事件的概率（probability），记为P（A），并规定：

公理1（非负性）　对于任意事件A，必有0≤P（A）≤1；

公理2（规范性）　必然事件的概率为P（Ω）=1；

公理3（可数可加性）　若A1，A2，…，An，…是互不相容的事件，则有

这一定义刻画了概率的本质，称为公理化定义.在这个定义出现之前曾有过概率的古典定义、统计定义，它们各适合一类随机现象.那么适合一切随机现象的概率的最一般定义应如何给出呢？很多人思索过这个问题.1900 年，大数学家戴维·希尔伯特（David Hilbert）在巴黎第二届国际数学家大会上公开提出要建立概率的公理化体系，即从概率的少数特性来刻画概率的概念.直到1933 年，苏联数学家柯莫哥洛夫在他的《概率论基本概念》一书中首次提出概率的公理化定义.这个定义概括了历史上几种概率定义中的共同特性，又避免了各自的局限性和含混之处，不管什么随机现象，只有满足定义中的三条公理才能说它是概率.这一公理化体系的出现迅速获得了举世公认，为现代概率论的发展打下了坚实基础，从此数学界才承认概率论是数学的一个分支.有了这个公理化体系后，概率论得到迅速发展，这个公理化体系是概率论发展史上的一个里程碑.

由概率的公理化定义可以推出概率的一些性质.

性质1　P（Ø）=0.

证　令An=Ø（n=1，2，…），

则

由概率的可数可加性得

而由P（Ø）≥0 及上式知P（Ø）=0.

这个性质说明，不可能事件的概率为0.但其逆命题不一定成立，我们将在第2章中加以说明.

性质2（有限可加性）　若A1，A2，…，An 为两两互不相容事件，则有

证　令An+1=An+2=…=Ø，则AiAj=Ø.当i≠j，i，j=1，2，…时，由可数可加性，得

性质3　设A，B 是两个事件，若A⊂B，则有

证　由A⊂B，知B=A∪（B-A），且A∩（B-A）=Ø.

再由概率的有限可加性有

又由P（B-A）≥0，得P（A）≤P（B）.(www.daowen.com)

性质4　对任一事件A，P（A）≤1.

证　因为A⊂Ω，由性质3 得P（A）≤P（Ω）=1.

性质5　对于任一事件A，有

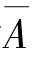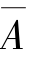证　因为 ∪A=Ω，∩A=Ø，

由有限可加性，得

性质6（加法公式）　对于任意两个事件A，B 有

证　因为A∪B=A∪（B-AB），且A∩（B-AB）=Ø.

由性质2，3 得

性质6 还可推广到三个事件的情形.例如，设A1，A2，A3 为任意三个事件，则有

一般地，设A1，A2，…，An 为任意n 个事件，可由归纳法证得

例1.14　掷3 次硬币，求至少一次正面朝上的概率.

解　假设A={至少一次正面}，则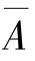={全是反面}，只包含一个样本点，基本事件总数为23=8.因此，P

例1.15　每个路口有红、绿、黄三色指示灯，假设各色灯的开闭是等可能的.一个人骑车经过三个路口，试求下列事件的概率：A=“三个都是红灯”=“全红”；B=“全绿”；C=“全黄”；D=“无红”；E=“无绿”；F=“三次颜色相同”；G=“颜色全不相同”；“颜色不全相同”.

例1.16　设一批产品共100 件，其中98 件正品，2 件次品，从中任意抽取3 件考虑两种取件方式：

（a）第一次取一个，观察后放回，搅匀后再取一个.这种称为有放回抽取.

（b）第一次取一个不放回，第二次从剩余的产品中再取一个.这种称为不放回抽取.

试分别就上面两种情形求：

①取出的3 件中恰有1 件是次品的概率.

②取出的3 件中至少有1 件是次品的概率.

解　设A 表示“取出的3 件中恰有1 件是次品”，设B 表示“取出的3 件中至少有1 件是次品”，

在条件（a）下：

在条件（b）下：