在n 次重复试验中，如果事件A 发生了m 次，则称为事件A 发生的频率（frequency）.同样，若事件B 发生了k 次，则为事件B 发生的频率.如果A 是必然事件，有m=n，即必然事件的频率是1.反之，不可能事件的频率为0.如果A 与B 互不相容，则事件A∪B 的频率为，它恰好等于两个事件的频率之和，这称为频率的可加性.

频率是否能够确切地描述事件发生的可能性大小呢？经验告诉我们多次重复同一试验，随机事件的频率具有稳定性.随着试验次数n 的增加，事件A 的频率会逐渐稳定于某个常数附近，而发生较大偏离的可能性很小.这种频率的稳定性就是定义概率的经验基础.这就是说频率不能确切地描述事件发生的可能性大小，但频率的稳定值可以描述.

为了说明频率稳定性，先来看一些著名的例子.

例1.6　抛掷一枚硬币，可能出现正面也可能出现反面，事先做出确定的判断是不可能的，但假如硬币是均匀的，那么我们有理由认为出现正面和反面的可能性应该一样，即在大量试验中出现正面和反面的频率都接近于0.5，为了验证这一点，历史上曾有不少人做过试验，如表1.2.

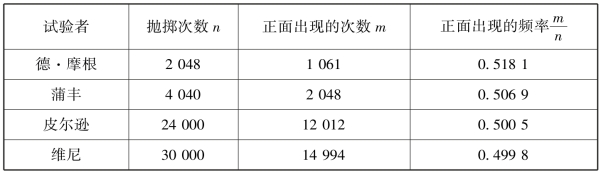
表1.2　历史上的掷硬币试验统计表

(www.daowen.com)

从表1.2 的数据可以看出：当抛掷次数较小时，频率的随机波动较大；随着抛掷次数的增大，频率呈现出稳定性；即当n 逐渐增大时，频率总是在0.5 附近摆动而逐渐稳定于0.5.

例1.7　对于新生婴儿的性别情况，很多人做了大量的统计.法国数学家拉普拉斯在《概率论哲学探讨》一文中指出，法国男婴出生率为.1935 年，瑞典数学家克拉美统计出瑞典的男婴出生率为0.518.我国的几次人口普查，得到类似的结论，男婴与女婴的比率为1.04∶1.这个例子指出，对于同一现象，不同时期、不同国家及不同的调查人得到的几个非常接近的数字表明：现象具有一定的规律性.

例1.6 和例1.7 的数据表明，随机现象有其偶然性的一面，也有其必然性的一面.这种必然性表现为大量试验中随机事件出现的频率的稳定性，即一个事件出现的频率常在某个固定的常数附近摆动，这种稳定性我们称为统计规律性.频率的稳定性说明随机事件发生的可能性大小是随机事件本身固有的，不随人们意志改变的一种客观属性，因此可以对它进行度量.

定义1.3　（概率的统计定义）在一定的条件下，事件A 在n 次重复试验中发生了m 次，当n 很大时，事件A 发生的频率m/n 稳定地在某一常数p 的附近摆动，且一般说来，n 越大，摆动幅度越小，则称这个常数p 为事件A 的概率，记作P（A）.

数值P（A）就是一次试验中事件A 发生的可能性大小的数量描述，它指出了事件概率的存在性，但并不能用这个定义计算事件的概率.实际中，人们常常采取大量试验的频率或用一系列频率的平均值作为事件的概率的近似值.这样定义的概率并不严格，而只是描述了一个大数定律，这是概率论中极限理论的雏形，它的严格讨论将放在本书的第5章给出.