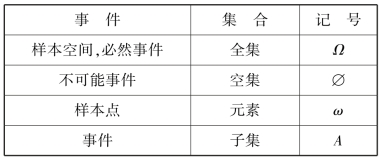
事件是一个集合，事件与集合的对应关系见表1.1.甚至，事件之间的关系与运算可以用集合之间的关系与运算来处理.

表1.1　事件与集合的对应关系

下面讨论事件之间的关系及其运算.

（1）事件的包含

如果事件A 发生必然导致事件B 发生，即属于A 的每一个样本点都属于B，则称事件B 包含事件A 或称事件A 包含于事件B，记作B⊃A 或A⊂B.

A⊂B 的等价说法是，如果B 不发生，则A 也不会发生.

对于任何事件A，有Ø⊂A⊂Ω.

若A⊂B 且B⊃A，则称事件A 与B 相等（或等价），记作A=B.

（2）事件的并（和）

两个事件A，B 中至少有一个发生，称为事件A 与B 的并事件或和事件，它是属于A 与B的所有样本点构成的集合，记作A∪B.

对任一事件A，有

事件的并可推广到多个随机事件的情形：

A=表示“A1，A2，…，An 中至少有一个事件发生”这一事件.

A=表示“可列无穷多个事件Ai 中至少有一个发生”这一事件.

（3）事件的交（积）

两个事件A 与B 同时发生，称为事件A 与B 的交事件或积事件.它是由A 与B 的所有公共样本点构成的集合，记作AB 或A∩B.

对任一事件A，有

B=表示“B1，B2，…，Bn n 个事件同时发生”这一事件.

B=表示“可列无穷多个事件Bi 同时发生”这一事件.

（4）事件的差

事件A 发生而事件B 不发生，称为事件A 与B 的差.它是由属于A 但不属于B 的那些样本点构成的集合，记作A-B.

由事件差的定义，立即得到：

对任一事件A，有

（5）互不相容（或互斥）事件

如果事件A 与B 不能同时发生，即AB=Ø，称事件A 与B 互不相容（或称事件A 与B 互斥）.从定义可以看出，互不相容事件A 与B 没有相同的样本点.

显然，基本事件间是互不相容的.

如果一组事件A1，A2，…，An，…中任意两个事件都是互不相容的，即AiAj=Ø（i≠j，i，j=1，2，…），则称事件A1，A2，…，An，…两两互不相容.

（6）对立事件

若A∪B=Ω 且A∩B=Ø，则称事件A 与B 互为对立事件（逆事件）.它是由样本空间中所有不属于A 的样本点组成的集合，记作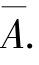

显然有

由互不相容事件和对立事件的定义可知，事件A 与B 若为对立事件，则它们一定是互不相容事件；反之不一定成立.

（7）完备事件组

若事件A1，A2，…，An 为两两互不相容事件，即AiAj=Ø（i≠j，i，j=1，2，…，n）并且A1 ∪A2∪…∪An=Ω，称A1，A2，…，An 构成一个完备事件组或构成样本空间的一个划分.该定义可推广到可数个随机事件的情形：若事件A1，A2，…，An，…为两两互不相容事件，即AiAj=Ø（i≠j，i，j=1，2，…）且A1∪A2∪…∪An…=Ω，称可数个事件A1，A2，…，An，…构成一个完备事件组或构成样本空间的一个划分.(www.daowen.com)

事件的关系及运算如图1.1—图1.6 所示.

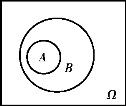
图1.1　A⊂B

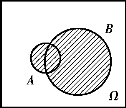
图1.2　A∪B

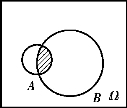
图1.3　A∩B

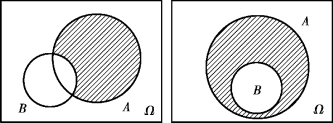
图1.4　A-B

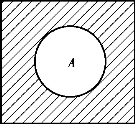
图1.5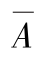　

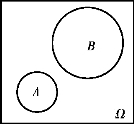
图1.6　AB=Ø

事件的运算和集合的运算有类似的性质.设A，B，C，是随机事件，则有以下运算定律：

①交换律：A∪B=B∪A，A∩B=B∩A.

②结合律：（A∪B）∪C=A∪（B∪C），（A∩B）∩C=A∩（B∩C）.

③分配律：A∪（B∩C）=（A∪B）∩（A∪C），A∩（B∪C）=（A∩B）∪（A∩C）.

④对偶律：

分配律和对偶律可以推广到任意个有限事件或无限多个事件上去，如：

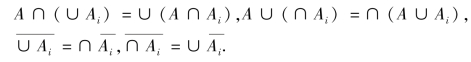
例1.4　掷一颗骰子的试验，观察出现的点数，A 表示“奇数点”，B 表示“点数小于5”，C表示“小于5 的偶数点”.用集合的列举表示法表示下列事件：Ω，A，B，C，A∪B，A-B，B-A，AB，AC，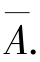

例1.5　从一批产品中每次取出一个产品进行检验（每次取出的产品不放回），事件Ai 表示第i 次取到的是合格品i=1，2，3.试用事件的运算符号表示下列事件：

①3 次都取到了合格品.

②3 次都没取到合格品.

③3 次中至少有一次取到合格品.

④3 次中恰有两次取到合格品.

⑤3 次中恰好有一次取到合格品.

⑥3 次中至少有两次取到合格品.

⑦3 次中至多有一次取到合格品.

解　①3 次都取到合格品：A1A2A3.

②3 次都没取到合格品：

③3 次中至少有一次取到合格品：A1∪A2∪A3.

④3 次中恰有两次取到合格品：A1A2

⑤3 次中恰好有一次取到合格品：A1

⑥3 次中至少有两次取到合格品：A1A2∪A1A3∪A2A3.

⑦3 次中至多有一次取到合格品：A1