物理学是一门建立在实验基础上的科学,物理定律是科学家从直接或间接的实验中、或者从对自然现象的长期观察中,探索归纳出来的规律。在物理学的发展过程中,科学家提出的新理论,必须经过实验的检验才能证明是否正确,或者是否需要修正。
作为学生,继承前人留给我们的物理知识时,为什么要做实验呢?主要有以下几点:
第一,物理概念是抽象的,我们通过实验能够从中获得建立概念的感性认识,这能帮助理解概念。例如,什么是瞬时速度、什么是加速度等,你动手测量它们以后,印象就深了。
第二,做实验就要使用仪器,学习使用基本测量工具、仪器,能够培养实际操作能力,这是今后从事实践工作的一项本领。
第三,物理定律是科学家经过长期艰苦的探索才归纳出来的,我们通过实验,就能够以较短的时间,大体经历一次科学探索的模拟过程,可以从中领悟到一些科学研究的方法,从而能提高对事物的分析研究能力,提高科学素质。
可见,不论是对于物理学的发展,还是对于我们学习物理,实验都是非常重要的。
一、有效数字
实验测量的结果是用数据反映出来的,但是必须要有科学的计数和计算方法,才能真实地反映实验成果。
1.仪器的精度与读数
以长度的测量为例,学生用的直尺最小分度为毫米,丈量土地用的卷尺一般最小分度为厘米,这最小分度就称为仪器的精度。显然,学生直尺比卷尺的精度高。
图1中用学生直尺测量小木块的长度,读数是33.9mm。这个读数中的“33mm”是准确可靠的,“0.9mm”是估计的不准确数。可见,用仪器进行测量所得的数据,是由准确的可靠数字和估计的不准确数字(也称为可疑数字)这两部分组成的。如果用丈量土地的卷尺测量长度,估计的读数应该在毫米(十分之一厘米)的位数。
有时用毫米精度的学生直尺测量某个长度刚好读到整数,如“40mm”(图2),其实这个整数也是估计的,正确读数应记为“40.0mm”。
从上面的例子可以看到,可疑数字前面的1位读数是对应仪器精度的。想一想,如果从某个电压表上测得的读数是2.54V,这个电压表的精度是多少?

图1

图2
2.有效数字
在每一次测量中,从仪器读得的全部可靠数字和最后1位可疑数字,它们都是有效的测量结果,叫做有效数字。例如,从图2中读得的“40.0mm”就是有效数字。实验记录应该用有效数字表示。如果以为小数点后面的“0”可有可无,对于图2,只记录“40mm”,就是自贬测量的精度——使其中的“0mm”表示成了可疑数字;而如果在读数后面随意添“0”,写成“40.00mm”就是夸大了测量精度——使其中的“40.0mm”都表示成了可靠数字。
3.有效数字位数的确定规则
(1)一切非零数字都是有效数字。如14.2是三位有效数字。
(2)在非零数字后面的零是有效数字。如1.0是两位有效数字,1.00是三为有效数字。
(3)在第一个非零数字前面的零不是有效数字。如0.1;0.01;0.001都是一位有效数字。
(4)有效数字的位数与单位换算无关。如:
100cm=10.0dm=1.00m 都是三位有效数字
10cm=1.0dm=0.10m 都是两位有效数字
10km=1.0×104m 都是两位有效数字
有效数字的运算规则:(https://www.daowen.com)
有效数字的运算有一定规则,本书对此不予要求。同学们对实验数据进行运算后,一般只需保留2~3个位数的数字,再配合用指数表示即可。例如,3.1×102 N、2.0×10-2V等。
二、误差
被测量的物理量有它的客观真实数据,叫做真值。在测量过程中由于仪器的性能、实验所采用的方法、自然环境、实验者的操作水平等原因,会导致测量值跟真值之间产生偏差,偏差的值就是误差。进行任何测量都会产生误差,这是客观事实。我们应该做的是研究误差产生的原因,设法减小误差;再就是计算实验中产生的误差大小,来评价实验的成果。
1.误差的分类
根据误差的性质及其产生的原因,可将误差分为系统误差和偶然误差两种。
(1)系统误差。由于仪器有缺陷(如零点未调好、刻度不准等),实验方法不完善,各人观察时的偏向(读数总是偏大或偏小)以及环境的变化(如压强、温度等变化的影响)等原因,引起多次测量结果总是有规律地偏大或偏小,这种误差称之为系统误差。例如,一个未经校正的电压表,它的指针不在零刻度,而是在0.1V处,那么它每次测量的读数都会偏大0.1V。
减小系统误差的方法,一般有:选用精度较高的仪器、使用仪器进行测量之前要进行校正、改善实验方法、提高操作技能等。
(2)偶然误差。偶然误差是由各种偶然因素对实验者、测量仪器、被测量物理量的影响而产生的。例如,用有毫米刻度的尺子量物体的长度,毫米以下的数值只能用眼睛来估计,各次测量的结果就不一致,有时偏大,有时偏小。再例如,进行电路测量时由于电源电压不稳定,会导致电表示数忽大忽小。
偶然误差的特点是测量结果总是有时偏大、有时偏小,并且偏大和偏小的概率基本相等。因此,我们可以多进行几次测量,各次测量数值的平均值就比一次测得的数值更接近于真实值。
2.误差的表示
误差的表示,就是把测量值跟真值进行比较。而真值也必须经过测量才能得知,但是只要进行测量就必然会有误差,因此被测对象虽然有一个客观的真值,我们却无法得知。解决问题的办法,就是用公认值代替真值,因为公认值是人们用精确的测量方法得到的。例如,初中的物理课本中给出的ρ水=1.0×103 kg/m3、ρ铝=2.7×103 kg/m3就是水和铝密度的公认值。在有些实验中,如测一个未知电阻的阻值时,它就没有公认值。在这种情况下,就把多次测量的算术平均值作为公认值。为什么算数平均值能作为公认值呢?因为每一次的测量值都在真值的附近,有时比真值偏大(正偏差),有时偏小(负偏差),把各次测量值相加求和,就可以使偏大、偏小相抵消。所以用测量值的和除以测量次数得出的算术平均值就很接近于真值。
以下表示的几种误差,都是把测量值跟公认值(或算术平均值)进行比较而确定的。
(1)绝对误差。测量值跟公认值之间总存在一定的差值,这个差值的绝对值叫绝对误差。
设对某物理量进行n次测量,测量值分别为x1,x2,…,xn,则该物理量的公认值(算术平均值)就是
![]()
每次测量的绝对误差分别为:![]()
各次测量的绝对误差的平均值叫平均绝对误差,用Δx表示,

通常Δx只取一位非零数字,测量的结果应写成如下形式:
![]()
例如,测量图1中的木块长度

木块长度实验值l=(33.8±0.1)mm。
(2)相对误差。仅由绝对误差的大小很难正确评价测量结果的优劣,还必须考虑测量物理量本身的大小。例如用直尺测量一张长度为100cm的桌子和20cm的铅笔,测量值分别为100.1cm和20.1cm两次测量得出的平均绝对误差相等,都是0.1cm,但前者占其公认值的0.1%,而后者占其公认值的0.5%。显然前者的精确度高。因为桌子比铅笔长,0.1cm的误差占总测量值的比例小。所以要反应实验的精确程度,就要看平均绝对误差跟平均值的比值有多大,这个比值就称为相对误差。一般用百分比来表示,又称为百分误差:
![]()
例如,上面举例中对小木块长度测量的相对误差为
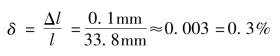
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






