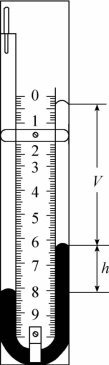
图2-4

在研究气体的性质时，人们最容易发现的是气体状态参量的变化。例如，皮球受热，皮球内气体的压强、体积、温度都会变化。把氧气装入钢罐中，氧气的这三个参量也会变化。内燃机气缸里的燃料混合物爆发时，这三个量也都变化等等。自然界和工程中所遇到的现象，大多数都是气体的压强、体积和温度这三个量同时发生变化的情况，只有两个量变化，另一个量不变化的情况也是有的。对于一定质量的气体，如果这三个量都不改变，我们就说气体处于一定的状态。如果这三个量或任意两个量同时变化，我们就说气体的状态改变了。那么，在气体状态改变时，这三个量的变化是任意的还是相互关联的，遵循一定的规律呢？实验证明，状态参量的变化是有规律的，这个规律就是本节讨论的中心问题。下面我们通过实验来研究一定质量的气体在状态变化时，这三个量的变化规律。

如图2-4所示，固定在刻度尺上一端封闭的U形玻璃管，其闭端（右上端）有一段被水银封在里面的气体柱。将U形管浸没在烧杯的水中，只留左端露出水面。改变水的温度，可以看出气体的体积和压强将同时发生变化。记下几组温度、体积和压强的数值，并将摄氏温度换算成热力学温度。计算每次测得的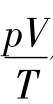值，并进行比较。我们可以发现，这个值是一个常量。由此可得出如下的结论：

一定质量的气体，它的压强和体积的乘积与热力学温度的比，在状态变化过程中始终保持不变，即

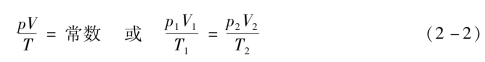
式中常量的大小取决于气体的质量和气体的种类。

精密实验指出，实际气体在状态变化过程中，并不完全符合由式（2-2）所确定的规律。随着压强的增大，温度的降低，所得结果与按式（2-2）计算出的数值偏差将越来越大。作为一种物理模型，我们把能够严格遵守式（2-2）规律的气体叫做理想气体。式（2-2）叫做理想气体状态方程，简称气态方程。在压强不太大，温度不太低的情况下，实际气体（如、氢、氧、氮、氦、空气等）均能较好地符合这一方程，可以当作理想气体处理。

对于一定质量的气体，在状态变化过程中，如果在p、V、T三个量中有一个量保持不变，那么根据气态方程，我们可以分别得出其余两个量之间的关系。

玻意耳-马略特定律 气体状态变化时，温度保持不变的过程叫做等温过程。根据气态方程（2-2）如果T1=T2，则

即一定质量的气体，在温度保持不变时，气体的压强与体积成反比。这个关系叫做玻意耳-马略特定律，它原是由英国科学家玻意耳（1627—1691）和法国科学家马略特（1620—1684）通过各自的实验独立发现的规律。

对一定质量的气体，在等温过程中压强和体积的关系，可以用分子动理论来解释。因压强与气体的分子密度和热力学温度成正比，当温度不变时，压强与分子密度成正比。所以当体积减半时，分子密度加倍，因而压强也增加一倍。反之，当体积加倍时，气体的压强减半。

盖吕萨克定律 气体状态变化时，压强保持不变的过程叫做等压过程。根据气态方程（2-2），如果p1=p2，则

即一定质量的气体，在压强保持不变时，气体的体积与热力学温度成正比。这一关系叫做盖吕萨克定律。它是法国科学家盖吕萨克（1778—1850）通过实验首先发现的。

查理定律 气体状态变化时，体积保持不变的过程叫做等体（积）过程。根据气态方程（2-2），如果V1=V2，则

即一定质量的气体，在体积保持不变时，气体的压强和热力学温度成正比。这个关系叫做查理定律。它是法国科学家查理（1746—1823）通过实验首先发现的。

如何用分子动理论解释盖吕萨克定律和查理定律，请同学们自己思考。

应当指出，上述气体三定律只适用于理想气体。实际气体只有在压强不太大、温度不太低的情况下，才能较好遵从这些规律。

例题1 在温度等于50℃而压强等于1.0×105 Pa时，内燃机里气态混合物的体积是930mL.如果经活塞压缩，气态混合物的压强增大到1.0×106 Pa，体积减小到155mL，那么气态混合物的温度将升高到多少？

分析 在应用气态方程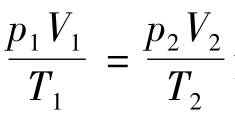解题时，由于P或V在等式中的可比性，它们的单位不一定都要统一成国际制单位，用其他非国际单位制的法定计量单位也可以，只要公式中同一物理量p或V的单位相同即可，而物理量T必须用K（开）作单位。

解 已知：V 1=930ml，p 1=1.0×105Pa，T 1=（273+50）K=323K，V 2=155ml，p 2=1.0×106Pa

求：T2(www.daowen.com)

依据气态方程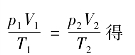

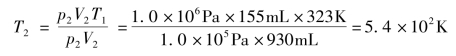
答：经活塞压缩后，气态混合物的温度将升高到5.4×102K。

例题2 如图2-5所示，在一端封闭粗细均匀的细玻璃管中，用16cm长的水银柱封入适量的空气，当把玻璃管竖直放置，开口向上时，管内空气柱长是15cm，这时大气压强p0=1.0×105Pa。当开口向下时，管内空气柱的长度是多少？

解 在上述过程中，可以认为温度保持不变，设玻璃管的横截面积为S，16cm高的水银柱产生的压强为ph

已知：p0=1.0×105 Pa，

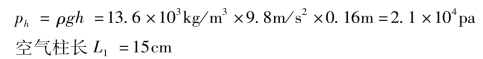
玻璃管竖直放置，开口向上时，空气柱的体积V1=L1 S，压强p1=p0+pk。开口向下时，空气柱的体积V2=L2S，压强p2=p0-pk

依据玻意耳-马略特定律，得

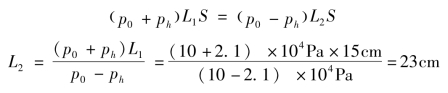
答：玻璃管向下竖直放置时，管内空气柱的长度是23cm。

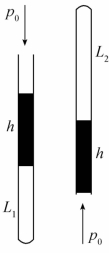
图2-5

习题2-1

1.分子动理论的基本内容是什么？

2.气体的压强是怎样产生的？怎样用分子动理论说明气体的压强与气体的分子密度和热力学温度的关系？

3.当一定质量的气体受热温度升高时，如果保持它的体积不变，气体的压强将怎么样变化？其原因是什么？如果要保持它的压强不变，气体的体积应怎样变化？为什么？

4.在下端封闭，粗细均匀的竖直玻璃管内，有一段4cm长的水银柱，水银柱的下面封闭着60cm的空气柱，如果在向管里装入20cm高的水银那么封闭在水银柱下面的空气柱是多高？（假设温度不变，大气压强是1.0×105 Pa）

5.一充有氦气的电灯泡，在温度为15℃时，灯泡内氦气的压强是1.0×106 Pa。当灯泡点亮后，若灯泡内温度升高到90℃，问这时灯泡内氦气的压强是多少？（可认为灯泡的体积不变）

6.贮气筒内有压缩气体，温度是20℃，压强是4.0×105Pa.如果从筒内放出一半质量的气体，并使筒内剩余的气体的温度降到-3℃，这些剩余气体的压强是多少？

7.如题图2-1所示，炮上所用的复位装置是利用炮的反冲后座使空气压缩，然后又利用此压缩空气使炮复位。设发炮前，装置内的空气的压强为4.5×107 Pa，温度为27℃，体积为7.6L。在炮反冲终了时空气的体积为2L，温度为127℃，求此时空气的压强。

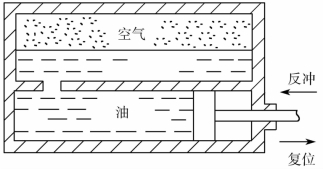
题图2-1