一、单摆

一根不能伸缩的细线（质量可忽略），其下端悬挂一个小球，上端固定在悬点上，小球略微移动后，就可以在一竖直平面内来回摆动，如图1-2所示，这种装置称为单摆。

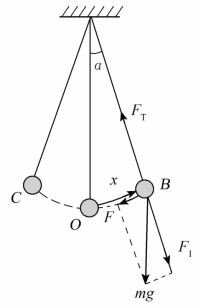
图1-2 单摆及受力分析

宿舍里电线悬挂着的电灯，也可以看作单摆，有趣的是，伽利略对单摆性质的研究，就是从悬挂着的灯开始的。1583年，伽利略在教堂里祈祷时，一个为灯添油的工人把灯碰了一下，然后油灯就持续地摆动起来。伽利略看着灯的摆动，猜想灯每摆一次用的时间是相等的。那时候没有钟表，伽利略利用脉搏跳动的次数来计时，证实了自已的猜想。当时，伽利略还只是一个18岁的学生。后来他利用摆的等时性制造了测量病人脉搏的计时器。以后还出现了摆钟——最早的现代计时器。

设摆球质量为m，摆长为L，即从悬点至小球球心的长度。摆角为α。摆球在运动过程中，受到重力mg和线的拉力FT的作用（为了简化问题，忽略阻力）。重力可分解为沿着悬线方向的分力F1和圆弧切线方向的力F。F1和线的拉力FT的合力沿摆线指向圆心（悬点），它只改变摆球运动的方向，不改变摆球运动的快慢，在研究单摆的摆动时，可以不予考虑。当α＜5°，圆弧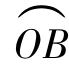可以近似地看成线段x。分力F可以近似地看作沿这条直线作用，它的方向指向平衡位置，它使摆球产生指向平衡位置的加速度。当小球运动到平衡位置的左侧时，其重力可以按同样方法进行分解，力F仍指向平衡位置。可见，力F是使单摆振动的回复力。

在摆角小于5°时，α角的弧度值近似等于sinα值，所以sinα≈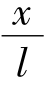，因此F=mg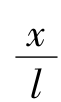。在考虑了力和位移的方向后

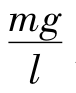是常量，用k表示，所以上式为

即在摆角小于5°的情况下，单摆振动的回复力跟位移成正比，而与位移的方向相反，所以，在摆角小于5°的情况下，单摆做简谐运动。在摆角大于5°的情况下，其振动规律要比简谐运动复杂得多。

二、单摆的周期

对于单摆，系数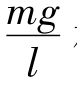相当于弹簧振子的劲度系数k，用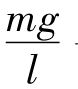去代替周期公式T=2π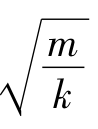中的k，得到

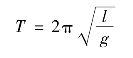
这就是单摆的周期公式，它说明：在偏角α＜5°情况下，单摆的周期与摆长的二次方根成正比，与重力加速度的二次方根成反比，而与摆球的质量和振幅无关。此式给出的单摆的周期完全由系统本身的性质决定，是系统的固有周期。(www.daowen.com)

由周期公式可以看出，在偏角很小的情况下，当单摆的摆长确定时，摆的振动周期就被确定了，而且与振幅无关，这种性质叫做单摆的等时性。利用单摆的等时性可以计时、制作钟表，还可以测定重力加速度。我们知道，重力加速度的测量是很复杂的，但用单摆这样简单的装置却可以来测量重力加速度：现代计时器可以准确地测量单摆的周期，再测出摆长，就能根据单摆的周期公式算出重力加速度g的值。

三、简谐运动的图像

为了便于研究物体的振动，常常画出振动的位移随时间变化的图像，这种图像叫振动图像。

如图1-3所示的装置：让一只装细沙的漏斗在一竖直平面里做简谐运动，再在漏斗的下面放置一块硬纸板，板上画有一根线Ot作为时间轴，这根线要通过摆的平衡位置并与摆的振动平面垂直。现在我们在漏斗摆动的同时匀速拉动纸板，从漏斗中漏下来的沙子就在纸板上记下了各个时刻摆的位置。任何一部分沙子跟Ot轴的垂直距离都等于该时刻摆的位移的大小，位移的最大值就等于单摆的振幅。沙子连续不断地漏下来，在纸板上就形成了摆的振动图像（位移-时间图像），如图1-4所示。实际上，所有简谐运动的图像都是余弦或正弦曲线。

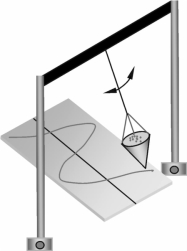
图1-3 砂摆

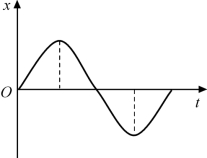
图1-4 简谐运动图像

【实践活动】

用单摆测脉搏

依照伽利略的办法，做一个单摆，测量一下自己的脉搏（例如让单摆振动50次，看脉搏跳动多少次）。然后用单摆公式算出单摆的周期，计算1分钟时间脉搏跳动的次数。再用表测一下脉搏，加以比较。

习题1-2

1.月球的重力加速度是地球重力加速度的0.17倍，周期为3s的摆钟到了月球上，周期会变为多大？

2.把一个单摆，在摆长减半、摆球质量减半、转移到月球上这三种情况下，它的周期会怎样变化？

3.半周期为1s的摆，称为秒摆。北京的重力加速度的大小为980.12cm/s2，请计算北京的秒摆摆长。（精确至0.01cm）