一、简谐振动

将一根轻弹簧一端固定，另一端系一物体，这个物体称为振子，这个系统就称为弹簧振子，如图1-1所示。振子开始静止在O点，O点就称为平衡位置。沿弹簧轴线把振子拉至B点，然后松手，振子就会以O点为中心左右振动起来。如果开始时把振子压至A点，松手后振子同样会振动起来。不过要注意，无论是拉还是压，都必须在弹簧的弹性限度以内。否则，弹簧振子就振不起来了。

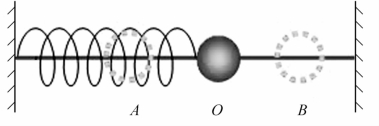
图1-1 弹簧振子

以平衡位置O点为原点，沿弹簧轴线向右的方向作为正方向。建立一个坐标系。这样，我们就可以定义一些物理量，来定量地描述和研究弹簧振子的振动规律了。

1.位移 振动物体离开平衡位置的位移x，称为振动物体的位移。位移是矢量，其方向由平衡位置指向物体所在位置。在上述坐标系中，物体在O点右侧，位移为正；物体在O点左侧，位移为负。

位移在SI中的单位是米，符号是m。

2.振幅 位移的最大值称为振幅，符号是A。振幅是表示振动强弱的一个物理量，是标量，并且只取正值。如果忽略振子和平面之间的摩擦，振子会在A、B两点间一直振动下去。在图1-1中，A点和B点在O点的两侧，并且对称。|OA|或|OB|就是振子的振幅。

在SI中，振幅的单位都是米，符号m。

3.回复力 我们可以分析一下振动过程中弹簧振子的受力情况：O→B，弹力方向向左，位移方向向右；B→O，弹力方向向左，位移方向向右；O→A，弹力方向向右，位移方向向左；A→O，弹力方向向右，位移方向向左。

可见，振子之所以能在平衡位置附近做往复的运动，原因是有一个方向总是指向平衡位置的弹力作用在振子上，我们把使物体回到平衡位置的力称为回复力。弹簧振子振动过程中弹力就是回复力。根据胡克定律，弹簧的弹力与弹簧的伸长量（或缩短量）成正比，即与小球离开平衡位置的位移x成正比，又因弹力总是与位移的方向相反，因此，弹力

负号表示回复力的方向与位移方向相反，k是弹簧的劲度系数。

物体在与位移成正比而与位移的方向相反的回复力作用下的振动，叫做简谐运动。

4.周期 从弹簧振子的某一状态起，当振子再次回到这一状态时，所完成的振动叫做一次全振动，如在图1-1中，O→B→O→A→O就是一次全振动。物体完成一次全振动所需的时间叫做周期。周期用T表示，是表征振动快慢的一个物理量。

周期是标量，在SI中的单位是秒，符号是s。

5.频率 振动物体在单位时间内完成全振动的次数叫做频率，用f表示。

频率是标量，在SI中的单位是赫兹，简称赫符号是Hz，一秒内完成一次全振动频率就是1Hz，1Hz=1s-1。频率也是表示振动快慢的一个物理量，它和周期的关系为

简谐运动的频率（或周期）与振幅无关，由振动系统本身的性质决定，所以叫做系统的固有频率（或固有周期）。对于做简谐运动的弹簧振子，它的固有周期和固有频率分别为：

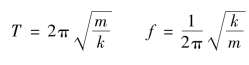
二、简谐运动的性质

根据牛顿第二定律，质量为m的振子的加速度a=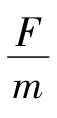=-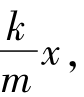即简谐运动中，加速度也跟位移成正比，而与位移的方向相反。这说明加速度的方向也始终指向平衡位置。(www.daowen.com)

简谐运动中，弹簧振子所受的弹力的大小和方向时刻改变，加速度的大小和方向也时刻改变，所以简谐运动是非匀变速运动。

弹簧振子的速度、加速度在一次全振动过程中是这样变化的。

（1）O→B，弹力增大，方向向左；位移增大，方向向右；速度减小，方向向右；加速度增大，方向向左。

（2）B→O，弹力减小，方向向左；位移减小，方向向右；速度增大，方向向左；加速度减小，方向向左。

（3）O→A，弹力增大，方向向右；位移增大，方向向左；速度减小，方向向左；加速度增大，方向向右。

（4）A→O，弹力减小，方向向右；位移减小，方向向左；速度增大，方向向右；加速度减小，方向向右。

三、简谐运动的能量

弹簧振子在运动过程中，只有弹力做功，机械能守恒。弹性势能和动能相互转化，总的机械能保持不变。

弹簧振子运动过程中能量的变化如下：

（1）O→B，速度减小，动能减小；位移增大，弹性势能增大。

（2）B→O，速度增大，动能增大；位移减小，弹性势能减小。

（3）O→A，速度减小，动能减小；位移增大，弹性势能增大。

（4）A→O，速度增大，动能增大；位移减小，弹性势能减小。

（5）平衡位置，位移为零，动能最大；振幅最大处，动能为零，弹性势能最大。

【实践活动】

观察木块在水面上的振动

在脸盆里盛上水，把一个小木块放进水中。用力压下木块然后松手，木块会上下振动起来。观察木块的振动规律，开始一段时间是不是接近简谐运动。再对木块进行受力分析，检验你的观察结论。

习题1-1

1.举一些你所见到的机械振动的实例。

2.描述机械振动的物理量有哪些？其含义分别是什么？

3.在图1-1中，若从A点开始计时，经过2.5个周期，振子在什么位置？（提示：振子经AO、OB、BO、OA用的时间是一样的）。