在干燥的环境中，很容易观察到由于摩擦而产生静电的现象。如用塑料梳子梳头，头发会随着梳子飘起来；脱衣服时听到噼啪的放电声等等。这些“电”到底有什么特点呢？

一、电荷守 电荷量

电荷的意思是物体带上了电，“荷”者“负荷”也，“电荷”是“电负荷”，即带上了电的意思，所以，物体带上了电，我们就说物体有了电荷。

自然界只存在两种电荷：正电荷和负电荷。同种电荷相互排斥，异种电荷相互吸引。物体所带电荷的多少叫做电荷量（简称电量），电荷量常用字母Q或q表示。在SI中电荷量的单位是库仑，简称为库，符号为C。

电荷量的值用正负数来表示，正电荷用正数表示，负电荷用负数表示，例如，甲物体带了3c的正电荷，记为q甲=+3c=3c，乙物体带3c的负电荷，记为q乙=-3c。

摩擦可以使物体带电，用丝绸摩擦过的玻璃棒上所带电荷叫做正电荷；用毛皮摩擦过的硬橡胶棒上所带电荷叫做负电荷。为什么物体间互相摩擦就会使物体带电呢？

因为物体是由分子组成的，分子是由原子组成的，如图5-1所示。原子核内的质子带正电，核外绕核高速旋转的电子带负电。正常情况下，物体内正负电荷数是一样多的，对外不显电性。当两个物体互相摩擦时，使物体中的正负电荷分开，电子发生转移，得到电子的物体带负电，而失去电子的物体带正电。

图5-1 原子结构

二、元电荷

经测定可知，一个质子和一个电子分别带有等量的正、负电荷，其电荷量的大小值为1.602×10-19 C，至今尚未发现比它们所带电荷量更少的电荷，因此，我们把这个最小的电荷叫做元电荷，用e表示。实验指出，任何带电体所带电荷量总是元电荷e的整数倍，即q=ne（n=±1，±2，±3，…）。电荷量e的数值最早是由美国物理学家密立根用实验测得的，他因测量元电荷（以及光电效应方面的研究）而获得1923年诺贝尔物理学奖。现在测得元电荷的精确值为

通常可取

三、真空中的库仑定律

正负两种电荷，同种电荷相斥，异种电荷相吸，而电荷间的相互作用力有多大？又与哪些因素有关呢？下面我们通过实验来研究。

如图5-2所示，把一个带正电的物体放在A处，然后把一个挂在丝线下端的带正电的小球先后挂在B、C、D各位置，带正电的小球受到斥力的大小，可以通过丝线对竖直方向的偏角大小显示出来。偏角越大，表示小球受到的斥力越大。实验表明，带正电的小球在B、C、D各点受到的斥力依此减小，可见电荷间的作用力随着距离的增大而减小。

增大丝线下端的带正电的小球的电量，在同一位置，小球受到的斥力也增大。可见电荷间的作用力随着电量的增大而增大。

通过实验还可证明，两个带电体间的相互作用还和两个带电体的大小、形状以及电荷在它上面的分布有关，同时又和它们周围的介质有关，情况比较复杂。为了简化问题，下面我们讨论两个点电荷在真空中的相互作用规律。

图5-2 库仑定律

所谓点电荷，是当带电体的大小比起它到其他带电体的距离要小很多时，这个带电体的几何形状和电荷的分布已无关紧要，即对电荷间相互作用力的影响可忽略不计，可以把它抽象成一个带电的几何点，物理上把这样抽象出来的，只有电荷量而没有大小和形状的点叫点电荷。

“点电荷”是一种理想化的模型，它是模仿力学的“质点”概念而建立的。严格理想化的点电荷应是一个带电的“几何点”，它是不存在的。但是只要带电体自身形体比它们间的距离小得多，以致带电体的形状和大小对相互作用力的影响可以忽略不计，这样的带电体就可以看成是“点电荷”。点电荷所带的电荷量不一定很小，有可能是很大的。

1785年，法国物理学家库仑（1736—180 6）根据库仑扭秤实验总结出了点电荷间相互作用的规律——真空中的库仑定律。

在真空中，两个点电荷q1和q2之间的相互作用力的大小，跟它们电荷量q1，q2的乘积成正比，跟它们之间的距离r的二次方成反比，作用力的方向在两个点电荷的连线上。这就是真空中的库仑定律。用公式表示为

(www.daowen.com)

式中k叫做静电力常量。在国际单位制中，F、q、r的单位分别是N、C、m，由实验可得k=9.0×109 N·m2/C2。

说明：（1）在应用库仑定律计算电荷间的相互作用力时，正、负电荷的电荷量用它们的绝对值，只计算作用力的大小，作用力的方向用同种电荷相互排斥，异种电荷相互吸引的规律去判断。（2）电荷间的相互作用力叫做静电力，又叫库仑力。（3）库仑力具有力的共性。如果同时存在两个以上点电荷，每两个电荷间的作用力仍由库仑定律决定，而每个电荷受到的总作用力则是其他电荷对它的作用力的矢量和。（4）F是q1与q2之间的相互作用力，q1对q2的作用力大小是F，q2对q1的作用力大小也是F，它们是一对作用力和反作用力，不论q1是否等于q2，它们都是大小相等方向相反。

例题 两个正、负点电荷，相距10cm，电荷量分别是+2×10-8 C和-3×10-8 C。它们在真空中的作用力是多少？如果把它们的距离变为30cm，它们间的作用力又是多少？

解 已知：q1=2×10-8 C，q2=3×10-8 C，r1=10cm=0.1m，r2=30cm=0.3m。

求：F1，F2

由公式F=得

当距离变成30cm时，因F∝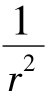，所以

由于q1和q2是异种电荷，所以F1和F2是引力。

答：它们间的作用力分别为5.4×10-4 N和6×10-5 N。

注：解F2的另一种方法是

阅读材料

库仑及库仑扭秤实验

库仑（1736—1806），法国工程师、物理学家。库仑在1773年发表了有关材料强度的论文，他提出使各种物体经受应力和应变直到它们的折断点的有关数据，然后根据这些资料就能计算出物体上应力和应变的分布情况。这种方法沿用至今，是结构工程的理论基础。1777年库仑开始研究静电和磁力问题。当时法国科学院悬赏，征求改良航海指南针中的磁针问题。库仑认为磁针架在轴上，必然会带来摩擦，要改良磁针的工作，必须从这一根本问题入手。他提出用细头发丝或丝线悬挂磁针。他又发现线扭转时的扭力和针转过的角度成比例关系，从而可利用这种装置算出静电力或磁力的大小。这个发现导致他发明了扭秤，扭秤能以极高的精度测出非常小的力。1779年库仑分析摩擦力，并提出有关润滑剂的科学理论。他还设计出水下作业法，类似于现代的沉箱作业法。1785—1789年，库仑用扭秤测量静电力和磁力，导出了著名的库仑定律。1806年8月23日库仑在巴黎逝世。

库仑扭秤实验装置的主要部分是一个扭力测微计M（如图5-3所示）。M下夹有一根细金属丝，在细金属丝下面悬挂一根玻璃棒，棒的一端有一个金属小球A，另一端有一个平衡小球B，在球A附近固定一个跟球A同样的金属小球C。如果球A和球C带同种电荷，它们间的斥力将使玻璃棒转过一个角度。要使玻璃棒回到原来的位置，必须向相反方向扭转旋钮M。这时金属丝的弹力产生的转动效果跟电荷间斥力产生的转动效果相抵消，从旋钮M转过的角度可以计算出电荷间作用力的大小。库仑用扭秤实验测得电荷间的作用力与电荷之间的距离二次方成反比。

图5-3 库伦扭秤

习题5-1

1.电荷量是4.8×10-8C的电荷中含有多少个元电荷？

2.真空中电荷量都是1C的两个点电荷相距1m，它们的静电力大小是多少？

3.在真空中有两个带电小球，一个的电荷量为+2.0×10-11 C，另一个的电荷量为-4.0×10-11 C，两球相距为0.1m时，它们之间的静电力有多大？

4.在真空中，电荷量为2.7×10-9 C的点电荷q1受到另一个点电荷q2的吸引力为8.0×10-5 N，q1、q2的距离为0.1m，求q2的电荷量是多少？

5.真空中的两个相同的金属小球，一个带的电荷量为4.0×10-9C，另一个带的电荷量为2.0×10-9C，把它们接触一下后分开，放在相距为1m的两点，它们之间的静电力有多大？