前面我们已学过牛顿第一定律、牛顿第二定律和牛顿第三定律，这三条定律统称为牛顿运动定律，以牛顿运动定律为基础的力学叫牛顿力学或经典力学。

17世纪以来，牛顿定律所奠定的经典力学得到了不断的发展，在科学研究和生产技术中得到了广泛的应用。经典力学与天文学相结合形成了天体力学，与工程实际相结合建立了各种应用力学，如水力学、材料力学、结构力学等工程力学。从行星的运动到汽车、火车、飞机等现代交通工具的运动；从抛出石块到发射导弹、卫星、航天飞机；从设计各种机械到拦河筑坝，建造桥梁和高楼大厦等，所有这些都服从牛顿力学的规律。牛顿力学能够在这样广阔的领域里用来解决实际问题，因而也就证明了牛顿力学的正确性。

经典力学是在（含有大量原子的）宏观物体低速运动（速度远小于光速）的情况下总结出来的规律，但是19世纪以后，随着科学技术的发展和实验手段的不断改进，人们观察到了许多经典力学的理论无法解释的新的现象和事实。

例如，人们发现高速运动的电子，其质量随速度的增大而增大，这一现象与经典力学的理论是不能相容的。直到20世纪初，著名物理学家爱因斯坦提出狭义相对论，建立了相对论力学，指出物体的质量、长度和物体运动过程的时间都与物体的速度有关，从而解决了经典力学无法解决的问题。相对论指出，物体的质量不是固定不变的，而是随着物体运动速度的增大而增大。设m0为物体静止时的质量，物体以速度v运动时，它的质量m用下式表示：

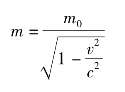
式中c表示光速。从这个公式可以知道，当物体运动的速度v远小于光速c时，即m≈m0，这时可认为物体的质量没有发生改变，仍等于它的静止质量，经典力学仍适用。太阳系里的一切宏观物体，如行星、卫星、人造飞船、地球上的各种交通工具，以及我们通常研究的物体，它们的速度都远小于光速，对这些物体的运动进行研究，使用牛顿力学已足够准确了。但是，当物体运动速度接近光速时，它的质量就远大于静止质量，例如v=0.8c时，m≈1.7m0；v=0.93c时，m=3.2m0。这表明经典力学在处理高速运动问题时就不再适用了，必须用相对论力学。因此，可以说，经典力学是相对论力学在低速情况下的良好近似。

此外，19世纪末、20世纪初，人们又发现一些微观粒子（如质子、中子、电子、原子等）不仅具有粒子性，还具有波动性，它们的运动规律不能用牛顿力学来解释，必须用量子力学来描述。对于宏观物体，牛顿力学和量子力学的差别也完全可以忽略，所以，又可以说，牛顿力学又是量子力学在宏观情况下的良好近似。

总之，牛顿力学只适用于解决宏观物体、低速运动物体的问题，不适用于解决微观粒子的高速运动问题。这就是牛顿力学的适用范围。

阅读材料

“站在巨人肩膀上的”牛顿

牛顿是英国著名的物理学家、数学家和天文学家，经典力学体系的奠基人。

1643年1月4日牛顿诞生于英格兰林肯郡的小镇乌尔斯索普的一个自耕农家庭。12岁进入离家不远的格兰瑟姆中学。1661年进入剑桥大学三一学院，1665年获学士学位。1669年10月27日巴罗便让年仅26岁的牛顿接替他担任卢卡斯讲座的教授。1672年起他被接纳为皇家学会会员，1703年被选为皇家学会主席。牛顿于1727年3月30日深夜在伦敦去世，葬在威斯敏斯特教堂，终年84岁。人们为了纪念牛顿，用他的名字来命名力的单位，简称“牛”。

牛顿的成就，恩格斯在《英国状况十八世纪》中概括得最为完整：“牛顿由于发明了万有引力定律而创立了科学的天文学，由于进行了光的分解而创立了科学的光学，由于创立了二项式定理和无限理论而创立了科学的数学，由于认识了力的本性而创立了科学的力学”。在这里，主要介绍牛顿在数学、光学、哲学（方法论）等方面所做的贡献。

Isaac Newton（1642—1727）

一、牛顿的数学成就

17世纪以来，原有的几何和代数已难以解决当时生产和自然科学所提出的许多新问题，例如：如何求出物体的瞬时速度与加速度？如何求曲线的切线及曲线长度（行星路程）？尽管牛顿之前已经有代数、解析几何、无穷级数等数学成就，但还不能圆满地解决这些问题。在笛卡尔的《几何学》和瓦里斯的《无穷算术》影响下，牛顿将古希腊以来求解无穷小问题的种种特殊方法统一为两类算法：正流数术（微分）和反流数术（积分），同时，他还在1676年首次公布了他发明的二项式展开定理。牛顿利用它还发现了其他无穷级数，并用来计算面积、积分、解方程等等。1684年莱布尼兹从对曲线的切线研究中引入了用拉长的S作为微积分符号，从此牛顿创立的微积分学在欧洲大陆各国迅速推广。

二、牛顿在光学上的成就

牛顿的《光学》是他的另一本科学经典著作（1704年）。该书集中反映了他的光学成就。

第一编是几何光学和颜色理论（棱镜光谱实验）。从1663年起，他开始磨制透镜和自制望远镜。在他送交皇家学会报告的信中说：“我在1666年初做了一个三角形的玻璃棱镜，以便试验那著名的颜色现象。为此，我弄暗我的房间……”接着详细叙述了他开小孔、引阳光进行的棱镜色散实验。关于光的颜色理论从亚里士多德到笛卡儿都认为白光纯洁均匀，乃是光的本色。“色光乃是白光的变种”。牛顿细致地注意到阳光不是像过去人们所说的五色而是在红、黄、绿、蓝、紫色之间还有橙、靛青等中间色，共七色。奇怪的还有棱镜分光后形成的不是圆形而是长条椭圆形，接着他又试验“玻璃的不同厚度部分”、“不同大小的窗孔”、“将棱镜放在外边”再通过孔、“玻璃的不平或偶然不规则”等的影响；用两个棱镜正倒放置以“消除第一棱镜的效应”；取“来自太阳不同部分的光线，看其不同的入射方向会产生什么样的影响”；并“计算各色光线的折射率”，“观察光线经棱镜后会不会沿曲线运动”；最后才做了“判决性试验”：在棱镜所形成的彩色带中通过屏幕上的小孔取出单色光，再投射到第二棱镜后，得出单色光的折射率（当时叫“折射程度”），这样就得出“白光本身是由折射程度不同的各种彩色光所组成的非均匀的混合体”。这个惊人的结论推翻了前人的学说，是牛顿细致观察和多项反复实验与思考的结果。在研究这个问题的过程中，牛顿还肯定：不管是伽利略望远镜（凹、凸透镜）还是开普勒望远镜（两个凸透镜），其结构本身都无法避免物镜色散引起的色差。他发现经过仔细研磨后的金属反射镜面作为物镜可放大30～40倍。1671年他将此镜送皇家学会保存，至今的巨型天文望远镜仍用牛顿式的基本结构。牛顿磨制及抛光精密光学镜面的方法，至今仍是不少工厂光学加工的主要手段。

《光学》第二编描述了光照射到叠放的凸透镜和平面玻璃上的“牛顿环”现象的各种实验。除产生环的原因他没有涉及外，他作了现代实验所能想到的一切实验，并作了精确测量。他把干涉现象解释为光行进中的“突发”或“切合”，即周期性的时而突然“易于反射”，时而“易于透射”，他甚至测出这种等间隔的大小，如黄橙色之间有一种色光的突发间隔为1/89000英寸（即现今2854×10-10米），正好与现代波长值5 710×10-10米相差一半!(www.daowen.com)

《光学》第三编是“拐折”（他认为光线被吸收）即衍射、双折射实验和他的31个疑问。这些衍射实验包括头发丝、刀片、尖劈形单缝形成的单色窄光束“光带”（今称衍射图样）等10多个实验。牛顿已经走到了重大发现的大门口却失之交臂。他的31个疑问极具启发性，说明牛顿在实验事实和物理思想成熟前并不先作绝对的肯定。牛顿在《光学》一、二篇中视光为物质流，即由光源发出的速度、大小不同的一群粒子，在双折射中他假设这些光粒子有方向性且各向异性。由于当时波动说还解释不了光的直进，他是倾向于粒子说的，但他认为粒子与波都是假定。

三、牛顿的哲学思想和科学方法

牛顿在科学上的巨大成就连同他的朴素的唯物主义哲学观点和一套初具规模的物理学方法论体系，给物理学及整个自然科学的发展，给18世纪的工业革命、社会经济变革及机械唯物论思潮的发展以巨大影响。这里只简略勾画一些轮廓。牛顿的哲学观点与他在力学上的奠基性成就是分不开的，对于一切自然现象，他都力图以力学观点加以解释，这就形成了牛顿哲学上的自发的唯物主义，同时也导致了机械论的盛行。事实上，牛顿把一切化学、热、电等现象都看作“与吸引或排斥力有关的事物”。例如他最早阐述了化学亲和力，把化学置换反应描述为两种吸引作用的相互竞争；认为“通过运动或发酵而发热”；火药爆炸也是硫磺、炭等粒子相互猛烈撞击、分解、放热、膨胀的过程，等等。

这种机械观，即把一切的物质运动形式都归为机械运动的观点，把解释机械运动问题所必需的绝对时空观、原子论、由初始条件可以决定以后任何时刻运动状态的机械决定论、事物发展的因果律等等，作为整个物理学的通用思考模式。可以认为，牛顿是开始比较完整地建立物理因果关系体系的第一人，而因果关系正是经典物理学的基石。牛顿在科学方法论上的贡献正如他在物理学特别是力学中的贡献一样，不只是创立了某一种或两种新方法，而是形成了一套研究事物的方法论体系，提出了几条方法论原理。在牛顿《原理》一书中集中体现了以下几种科学方法：

（1）实验——理论——应用的方法。牛顿在《原理》序言中说：“哲学的全部任务看来就在于从各种运动现象来研究各种自然之力，而后用这些方去论证其他的现象。”科学史家I.B.Cohen正确地指出，牛顿“主要是将实际世界与其简化数学表示反复加以比较”。牛顿是从事实验和归纳实际材料的巨匠，也是将其理论应用于天体、流体、引力等实际问题的能手。

（2）分析——综合方法。分析是从整体到部分（如微分、原子观点），综合是从部分到整体（如积分，也包括天与地的综合、三条运动定律的建立等）。牛顿在《原理》中说过：“在自然科学里，应该像在数学里一样，在研究困难的事物时，总是应当先用分析的方法，然后才用综合的方法……。一般地说，从结果到原因，从特殊原因到普遍原因，一直论证到最普遍的原因为止，这就是分析的方法；而综合的方法则假定原因已找到，并且已经把它们定为原理，再用这些原理去解释由它们发生的现象，并证明这些解释的正确性”。

（3）归纳——演绎方法。上述分析一综合法与归纳一演绎法是相互结合的。牛顿从观察和实验出发。“用归纳法去从中作出普通的结论”，即得到概念和规律，然后用演绎法推演出种种结论，再通过实验加以检验、解释和预测，这些预言的大部分都在后来得到证实。当时牛顿表述的定律他称为公理，即表明由归纳法得出的普遍结论，又可用演绎法去推演出其他结论。

（4）物理——数学方法。牛顿将物理学范围中的概念和定律都“尽量用数学表出”。爱因斯坦说：“牛顿才第一个成功地找到了一个用公式清楚表述的基础，从这个基础出发他用数学的思维，逻辑地、定量地演绎出范围很广的现象并且同经验相符合”，“只有微分定律的形式才能完全满足近代物理学家对因果性的要求，微分定律的明晰概念是牛顿最伟大的理智成就之一”。牛顿把他的书称为《自然哲学的数学原理》正好说明这一点。

牛顿对世界发展和科学技术的进步的贡献是众所周知，但他对自己的成就是怎样认识的呢？他说：“我不知道世上的人对我怎么评价。我却这样认为：我好象是站在海滩上玩耍的孩子，时而拾到几块莹洁的石子，时而拾到几片美丽的贝壳并为之欢欣。那浩瀚的真理的海洋仍然在我的前面未被发现。”“如果我所见的比笛卡儿要远一点，因为我是站在巨人们的肩膀上的缘故。”牛顿的这种谦虚精神永远值得后人敬仰和学习。

习题3-4

1.要使质量是2×104 kg的火车厢以0.2m/s2的加速度前进，要对火车施加多大的牵引力？设火车厢行进中受到的阻力是车厢重量的0.002倍。（取g=10m/s2）

2.一架喷气机，载客的总质量为1.0×105kg，喷气机的总推力为1.7×105N，飞机滑行时所受阻力为1.0×104 N，飞机在水平跑道上滑行了50s后起飞，求飞机起飞时的速度和起飞前的位移。

3.质量为50kg的男孩，站在升降机里，当升降机以2m/s的速度匀速上升时，男孩对地板的压力大小是多少？当升降机以1m/s2的加速度匀加速上升时，男孩对地板的压力大小是多少？当升降机以-1m/s2的加速度匀减速上升时，男孩对地板的压力大小又是多少？（取g=10m/s2）

4.位于水平面上质量为m的木块，在大小为F、方向与水平方向成α角的拉力的作用下，沿水平面做匀加速直线运动，如题图3-1所示。若木块与水平面间的动摩檫因数为μ，则木块的加速度的大小是多少？

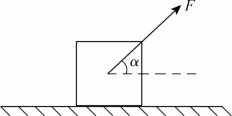
题图3-1 位于水平面上的木块

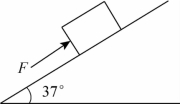
题图3-2 沿斜面向上推物块

5.在倾角为37°的斜面上有一质量为5kg的物体，物体与斜面之间的动摩檫因数为0.1。给物体一个与斜面平行向上的推力，推力的大小为39N，求物体的加速度是多少？（取g=10m/s2，sin37°=0.6，cos37°=0.8）