一、力的分解

1.力的分解

求一个已知力的两个分力叫做力的分解。

力的分解就是已知平行四边形的对角线，按平行四边形定则求出两个邻边。如果没有条件限制，邻边可以有无数组，即可求出无数对大小、方向不同的分力。如图2-26所示。显然这是没有意义的。那么，怎样才能使力的分解有确定的结果呢？

2.力的分解有确定结果的条件

一般来说，要使一个力的两分力是唯一的，必须满足下列条件之一：

（1）已知二分力的方向。

如图2-27（a）所示，F为已知力，两条虚线为二分力的方向。这种情况下，我们可以过F的末端分别作两条虚线的平行线，得到平行四边形F1 OF2 F，与已知力F共点的平行四边形的两个邻边OF1、OF2就表示要分解出的两个分力F1和F2，如图2-27（b）所示。

图2-26 力分解的不确定性

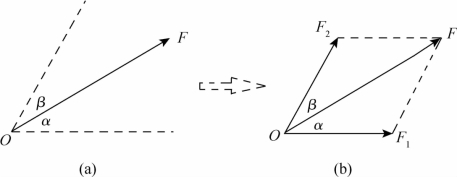
图2-27 已知二力的方向分解已知力

（2）已知二分力中一个分力的大小和方向。

如图2-28（a）所示，F为已知力，F1为已知力F的一个分力。这种情况下，我们先把F和F1的末端用虚线连结起来，过O作FF1的平行线；再过F末端作F1的平行线，得到平行四边形F1OF2F，OF2就表示F的另一个分力F2，如图2-28（b）所示。

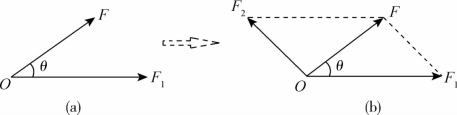
图2-28 已知一个分力的大小和方向分解已知力

那么，一个力究竟应该如何分解才能更好地解决实际的问题呢？这要根据讨论的问题的具体情况来确定。

二、分解力的两种方法

1.根据力的作用效果分解力

例如，把一个物体挂在互成角度的两根绳子上，物体的重力G产生两个效果：物体沿绳AO和BO拉紧绳子。要知道拉这两根绳子的力有多大，就要求出重力G在AO和BO方向上的两个分力。如图2-29（a）所示。

具体作图的方法是：先画重力G，再延长AO和BO，最后过重力G的末端作AO和BO方向的平行线（虚线），构成一个平行四边形。两条虚线在AO和BO方向截取的两段线段就是这两个方向上的分力F1和F2。如图2-29（b）所示。

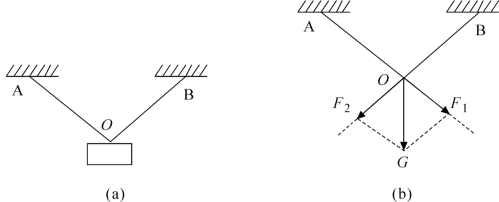
图2-29 按力的效果分解已知力

又例如，放在斜面上的物块，其重力G产生两个效果：使物块沿斜面向下滑动，同时使物块压紧斜面。因此，可以沿着这两个方向分解重力G。

2.力的正交分解

在实际中，一个已知力往往只产生两个作用效果，并且这两个作用效果方向互相垂直，所以，我们专门把这种情况拿出来讨论，给它起了个名字叫力的正交分解。把一个力沿着互相垂直的方向分解，叫做力的正交分解。如图2-30所示是把一个与水平方向成α角，斜向右上方的力F向水平方向和竖直方向分解的示意图，力F沿水平方向的分力F1和竖直方向的分力F2后分别为：

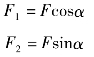(www.daowen.com)

例如，对斜面上的物体，按重力的两个作用效果，沿斜面向下和垂直于斜面向上两个方向，对在斜面上的物体的重力G进行正交分解，如图2-31所示，由图可知，重力沿斜面使物体下滑的分力G1和垂直于斜面的分力G2的大小分别为

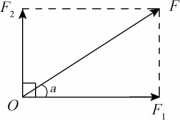
图2-30 力的正交分解

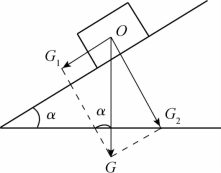
图2-31 力的正交分解

例题 有一木箱放在水平地面上，一个人用大小为300N，方向与水平方向成30°角斜向右上方的力拉木箱，如果按照作用效果分解此力，应该如何分解？两个分力的大小是多少？

分析：人的拉力产生两个作用效果，一个是使木箱沿水平地面向前滑动；另一个是把木箱竖直向上提，减小木箱对地面的压力。所以，人的拉力应该沿水平方向和竖直方向分解，如图2-32所示。

解 已知：F=300N，α=30°

求：F1，F2

将F向水平方向和竖直方向分解

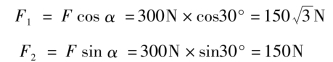
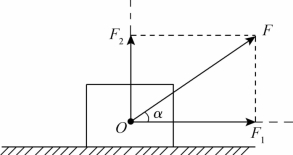
图2-32 斜向右上方拉力的分解

答：按照作用效果此力应该沿水平方向和竖直方向分解，水平方向分力的大小为150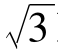N，竖直方向分力的大小为150N。

如果一个人用与水平方向成30°斜向右下方的力推木箱，又应该如何分解此力？同学们自己做一做看。

习题2-7

1.一个骑自行车的人，沿倾角θ=30°的斜坡向下滑行，人和车共重为G=700N，计算重力沿斜面方向的分力和垂直斜面方向的分力。

2.水平地面上有一木箱，甲用水平力F推着它走，乙用水平力F拉着它走，丙用倾斜向下的力F推着它走，丁用倾斜向上的力F拉着它走。哪一种情况的滑动摩擦力最小？

3.画出题图2-8（a）、（b）中合力F的分力。

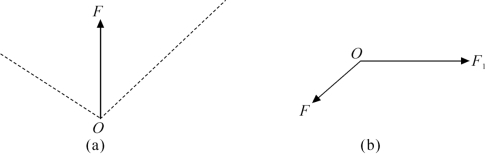
题图2-8 已知合力求分力

4.如题图2-9所示，木箱重200N，放在水平地面上，一个人用大小为100N与水平方向成60°斜向下的力推木箱，木箱沿地平面匀速运动。问：人给木箱的水平推力和竖直向下的压力各是多少？

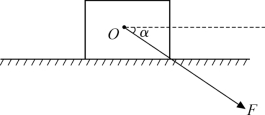
题图2-9 斜面下推力的分析