对于现代时间序列计量经济学而言，I（0）与I（1）是两个非常重要的概念。在应用中，当对单变量建模时，通常要求序列为I（0）过程，而在对多变量进行协整分析时，则一些变量可能是I（1）过程。然而，迄今为止，对于I（0）与I（1）过程的界定，仍没有一致公认的说法。计量经济学家从不同的研究角度对I（0）与I（1）过程给予了不同的解释。Davidson（2010）总结了已有文献中引用次数较高的五种关于I（0）的界定。

（1）一个时间序列经过d次差分后，不含有确定性成分，并且可由一个平稳可逆的ARMA过程来表示，则该序列为I（d）过程。（Engle和Granger，1987，p.252）

（2）短记忆时间序列为I（0）过程，因为这个序列不需要进行差分。（Engle和Granger，1991，p.3）

（3）如果一个时间序列经过k次差分后恰好变得平稳，则这个序列是I（k）过程，因此平稳序列即I（0）过程。（Banerjee等，1993，p.7）

（4）一个没有累计过去误差，并且具有有限非零方差的时间序列，可以称为I（0）过程。（Hendry，1995，p.43）

（5）一个随机过程ty满足，并且在时收敛，以及，εt～iid（0，σ2），则yt为I（0）过程。（Johansen，1995，p.34～35）

从上述五种界定看，第（2）～（4）种说法都仅描述了I（0）过程所具有的其中一个特征，分别是短记忆性、平稳性以及有限方差。从本质上看，这三种说法并不是I（0）过程非常正式的定义，同时，这三种特征也并非等价的，从这三个定义上，也看不出I（0）过程的这三个特征彼此之间有什么联系。相比之下，第（1）种说法与第（5）种说则更为严密一些，并且也将I（0）过程所具有的这三个特征整合在了一个体系下。但是，Davidson（2010）指出，I（0）的这两个较为严密的界定，也只是将注意力集中在了一部分线性模型上，也就是说，只有一部分线性I（0）过程才完全具有上述这三个特征，而对于更为一般的线性I（0）及非线性I（0）过程而言，这三个特征并不一定也没有必要完全具备。一个典型的例子是趋势平稳过程，I（0）［或I（1）］过程是针对随机项而言的（Stock，1994），所以，趋势平稳过程是I（0）过程，但却不是平稳过程；而分整过程I（d），当d＜0.5时为平稳过程，但却不是I（0）过程。由此可见，平稳性既不是I（0）过程的必要条件也不是充分条件。

另外一类界定I（0）与I（1）过程的方法，是从渐近理论出发，通过推导数据生成过程或数据的部分和过程（partial sum process of the data）的渐近分布来区分I（0）与I（1）过程。具有代表性的文献是Stock（1994）、Müller（2008）以及Davidson（2002，2010），下面分别简单介绍这三种界定。

Stock（1994）关于I（0）与I（1）过程的界定：

令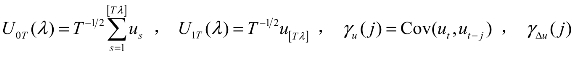=Cov（Δut，Δut-j），其中[·]表示不超过最大整数函数，则定义I（0）与I（1）分别为

式中，W（·）表示定义在［0，1］区间上的标准布朗运动。

Müller（2008）关于I（0）与I（1）过程的界定：

对于序列yt，当且仅当时，ty为I（0）过程；当且仅当时，ty为I（1）过程，其中，σ＞0。

Davidson（2002，2010）关于I（0）与I（1）过程的界定：

对于时间序列tx，以及定义在（0，1］区间上的部分和过程^[1]：(www.daowen.com)

当且仅当XT（ξ）⇒W（·）时，定义序列xt为I（0）过程；当且仅当YT（ξ）⇒W（·）时，定义序列xt为I（1）过程。

上述三种定义表明，任何满足泛函中心极限定理的一个异质过程，都可能是I（0）过程，而增量（increments）为I（0）过程的序列则是I（1）过程。这种定义方式的直观含义是：I（0）过程需要“积分”（或求累加和）一次才能变成I（1）过程，而I（1）过程无须“积分”，本身就满足泛函中心极限定理。从本质上看，这三种定义是等价的，而Davidson（2002，2010）对于I（0）过程的定义在形式上更为一般化，其不仅涵盖了所有线性I（0）过程，也将非线性I（0）过程纳入其中。在Stock（1994）与Müller（2008）的定义中，序列均剔除了确定性成分，而式（4.3）中含有序列的均值，因此，趋势平稳过程也适用于此定义。此外，这种定义方式对于非线性而言非常重要，Davidson（2002）的研究表明，一些常用的非线性模型，如双线性模型、GARCH模型、TAR模型以及STAR模型也都适用于此定义，并且指出，在非线性I（0）过程中并不排除存在协方差不平稳的情况，只要这种情况不是全局的（global）特征即可。这种情况在TAR模型和STAR模型中经常会出现，如在一个两区制的TAR模型中，一个区制是单位根过程，而另外一个区制是协方差平稳过程，Caner和Hansen（2001）称之为“局部单位根”（partial unit root）过程，但并不是单位根过程，该过程仍然满足式（4.3），因此属于I（0）过程，可以简单称其为整体平稳过程。同样，对于STAR模型，本书第3章讨论的局部非平稳而整体平稳的过程，也属于此类情况。

另一个关心的问题是：是否存在非线性单位根过程？如果存在，如何表示？如何检验？

如果存在非线性单位根过程，那么在对其进行检验时，检验式的形式应当是非线性的，并且原假设的形式也应当是非线性的，否则就退化成了线性单位根的检验。但从已有的文献看，在涉及单位根过程与非线性I（0）过程的区分检验中，原假设都是线性单位根过程，可见，对于非线性单位根问题，仍然存在许多未知的领域。下面简单分析非线性单位根的生成过程。

考虑数据生成过程：（1-L）（1-φtL ）yt=εt，εt～iid（0，σ2），将其展开为

式中，φt为可变参数，可以表示为内生变量或外生变量的函数，从式（4.5）可以得到一个类似于特征多项式的表达式：（1-L）（1-φtL）=0，当θt的取值不依赖于yt时，该表达式即特征多项式，则可知yt中含有单位根；如果φt的取值依赖于yt的滞后项，如TAR模型、STAR模型等，则（1-L）（1-φtL）=0不是真正意义上的特征多项式，但由于我们约束了φt的取值在［0，1］区间，因此，yt仍有可能是含有单位根的过程。以两区制的TAR模型为例，φt的取值为0或者1，当φt取0时，yt为I（1）过程；当φt取1时，yt为I（2）过程。因此，总体而言，yt是一个含有单位根的非线性过程，根据式（4.4）对I（1）过程的界定，此时，yt为非线性I（1）过程。由此我们推测，诸如TAR模型、STAR模型这类存在不同区制，并且不同区制具有不同单整阶数的非线性随机过程，其整体单整阶数可能取决于局部区制单整阶数的最小值。

上述的分析表明，理论上确实存在非线性单位根过程，但在STAR模型中是否存在非线性单位根过程仍不得而知。同时，如何检验非线性单位根过程却是相当困难的，因为对于大多数非线性过程而言，平稳遍历性、矩的存在性以及总体矩的特征等是未知的，更为重要的是，非线性单位根过程的渐近理论至今仍没有形成。因此，本书在下面的单位根检验研究中，不考虑非线性单位根的情况，也就是说，对于一个时间序列而言，只考虑三种可能的数据生成过程：线性单位根、线性I（0）过程以及非线性I（0）过程。尽管如此，下面仍然将涉及非线性形式单位根检验的文献做简单梳理。

Granger 等（1997）研究了非线性的随机趋势，他们给出了如下非线性随机趋势生成过程的一般表达式：

式中，g与σ2是非线性的平滑函数。Granger等（1997）研究了几种常见非线性函数下的非线性随机趋势生成机制，以及在这些函数下，数据能表现出具有生长特性所具备的条件。他们也注意到非线性单位根问题，但很明显，式（4.6）无法从解析角度给出序列是否含有单位根，对此，他们采用模拟方式分析了式（4.7）的非线性随机趋势。

他们给出了α和β几组不同的取值，然后估计式（4.9）中（φτ-1）所对应的t统计量及其核密度分布，通过与ADF统计量的分布相比较发现，在α和β取某些特定的值时，t统计量分布与ADF分布很相似。可以看出，这种方法并不能检验Xt是否含有单位根，因为ADF本身是一个线性单位根检验方法，而式（4.9）是一个非线性模型，此外，并非在α和β所有的取值中都能得到近似于ADF分布的t统计量分布，这只是局部的一些特征，整体上是否是非线性单位根过程，他们在文章中并没有明确回答。

Park和Phillips（1999，2001）研究了回归变量是单位根过程的非线性回归问题，推导出了一系列单位根过程的非线性转换函数的渐近理论，为非线性协整理论的发展奠定了基础。他们的基本模型是：yt=g（xt，θ）+ut，其中xt是线性单位根过程，g表示非线性单调变换函数，ut是鞅差分过程，θ表示参数向量。但Park和Phillips（2001）明确指出xt不包括yt-1，即他们的理论并不适用于yt=g（yt-1，θ）+ut情形，因为如果yt-1是单位根过程，而对其进行非线性变换，未必仍然会得到一个单位根过程。因此，Park和Phillips（1999，2001）中一系列单位根过程的非线性转换函数的渐近理论并不适用于非线性单位根过程。

Gao 等（2008）考虑了一类非线性自回归模型：Xt=g（Xt-1）+εt，εt～iid（0，σ2），g表示未知的非线性函数，将其变换为如下非线性随机游走过程^[2]：

式中，g1（Xt-1）为能够识别的非线性函数，他们采用非参数方法检验H0。可以看出，如果H0没有被拒绝，则式（4.10）依概率收敛于随机游走过程，而不是非线性单位根过程，所以，此方法仍是对线性单位根进行检验，根本无法获悉序列Xt是否为非线性单位根过程。

此外，Caner和Hansen（2001），Kapetanios等（2003），Bec等（2004），Park和Shintani（2016），Bec等（2008）等都在TAR或者STAR模型框架下研究了线性单位根检验问题。